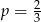W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę z tej grupy. Prawdopodobieństwo tego, że będzie to kobieta, jest równe
A) 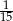 B)
B) 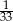 C)
C) 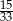 D)
D) 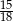
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo
W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę z tej grupy. Prawdopodobieństwo tego, że będzie to mężczyzna, jest równe
A) 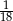 B)
B) 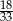 C)
C) 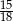 D)
D) 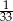
W grupie 60 osób (kobiet i mężczyzn) jest 35 kobiet. Z tej grupy losujemy jedną osobę. Prawdopodobieństwo wylosowania każdej osoby jest takie samo. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy mężczyznę, jest równe
A) 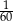 B)
B) 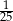 C)
C) 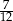 D)
D) 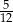
W grupie liczącej 29 uczniów (dziewcząt i chłopców) jest 15 chłopców. Z tej grupy trzeba wylosować jedną osobę. Prawdopodobieństwo zdarzenia polegającego na tym, że zostanie wylosowana dziewczyna, jest równe
A) 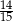 B)
B) 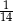 C)
C) 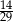 D)
D) 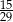
Wiadomo, że 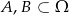 oraz
oraz 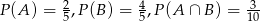 . Zatem:
. Zatem:
A) 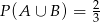 B)
B) 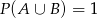 C)
C) 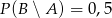 D)
D) 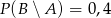
Wiadomo, że 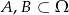 oraz
oraz 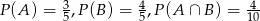 . Zatem:
. Zatem:
A) 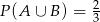 B)
B) 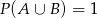 C)
C) 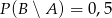 D)
D) 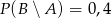
W pudełku jest 40 kul. Wśród nich jest 35 kul białych, a pozostałe to kule czerwone. Prawdopodobieństwo wylosowania każdej kuli jest takie samo. Z pudełka losujemy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy kulę czerwoną, jest równe
A)  B)
B) 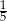 C)
C) 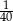 D)
D) 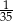
W pudełku jest 60 kul. Wśród nich jest 27 kul białych, 18 kul niebieskich, a pozostałe to kule żółte. Prawdopodobieństwo wylosowania każdej kuli jest takie samo. Z pudełka losujemy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy kulę, która nie jest niebieska, jest równe
A) 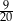 B)
B) 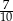 C)
C) 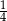 D)
D) 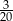
Rzucamy dwiema kostkami do gry. Jeśli 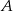 oznacza zdarzenie „suma wyrzuconych oczek jest równa 11”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 11”, a 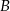 oznacza zdarzenie „suma wyrzuconych oczek jest równa 9” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 9” to
A) 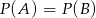 B)
B) 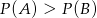 C)
C) 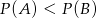 D)
D) 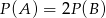
Rzucamy dwiema kostkami do gry. Jeśli 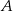 oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a 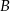 oznacza zdarzenie „suma wyrzuconych oczek jest równa 8” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 8” to
A) 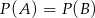 B)
B) 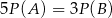 C)
C)  D)
D) 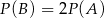
Rzucamy dwiema kostkami do gry. Jeśli 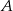 oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a 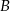 oznacza zdarzenie „suma wyrzuconych oczek jest równa 11” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 11” to
A) 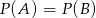 B)
B) 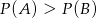 C)
C) 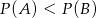 D)
D) 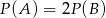
Rzucamy dwiema kostkami do gry. Jeśli 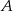 oznacza zdarzenie „suma wyrzuconych oczek jest równa 6”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 6”, a 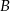 oznacza zdarzenie „suma wyrzuconych oczek jest równa 10” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 10” to
A) 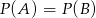 B)
B) 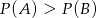 C)
C) 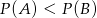 D)
D) 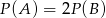
W pokoju w kilkunastu ponumerowanych workach znajdują się kolorowe piłki. Miłosz z zamkniętymi oczami wybiera losowo jeden z tych worków, a potem z wybranego worka wybiera jedną piłkę. Prawdopodobieństwo wybrania białej piłki z worka numer 1 jest równe 0,3, a prawdopodobieństwo, że Miłosz wybierze worek numer 1 jest równe 0,4. Jakie jest prawdopodobieństwo tego, że Miłosz wybierze worek numer 1 i z tego worka wyjmie piłkę, która nie jest biała?
A) 0,7 B) 0,9 C) 0,12 D) 0,28
Z grupy 72 osób (kobiet i mężczyzn) losujemy jedną osobę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy mężczyznę, jest równe  . Liczba kobiet w tej grupie jest równa
. Liczba kobiet w tej grupie jest równa
A) 24 B) 48 C) 36 D) 12
Zdarzenia 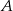 i
i 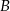 zawarte w zbiorze zdarzeń elementarnych
zawarte w zbiorze zdarzeń elementarnych 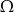 spełniają warunek
spełniają warunek 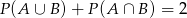 . Zatem
. Zatem
A) 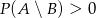 B)
B) 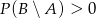 C)
C) 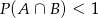 D)
D) 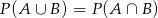
Zdarzenia 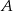 i
i 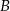 zawarte w zbiorze zdarzeń elementarnych
zawarte w zbiorze zdarzeń elementarnych 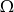 spełniają warunek
spełniają warunek 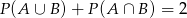 . Zatem
. Zatem
A) 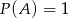 B)
B) 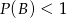 C)
C) 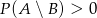 D)
D) 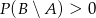
W urnie zawierającej kule białe i czarne jest 60 kul. Losujemy jedną kulę. Jeśli prawdopodobieństwo wylosowania kuli białej jest równe  , to kul czarnych w tej urnie jest
, to kul czarnych w tej urnie jest
A) 30 B) 24 C) 20 D) 36
W pudełku są tylko kule białe, czarne i zielone. Kul białych jest dwa razy więcej niż czarnych, a czarnych jest trzy razy więcej niż zielonych. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe
A)  B)
B) 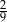 C)
C)  D)
D) 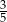
W pudełku są tylko kule białe, czarne i zielone. Kul białych jest dwa razy więcej niż czarnych, a czarnych jest trzy razy więcej niż zielonych. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli czarnej lub białej jest równe
A)  B)
B) 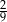 C)
C) 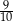 D)
D) 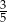
Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych oczek wyniesie co najwyżej 9, jest równe
A) 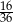 B)
B) 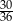 C)
C) 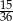 D)
D) 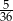
Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych oczek wyniesie co najwyżej 10, jest równe
A) 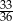 B)
B) 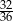 C)
C) 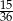 D)
D) 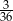
Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych oczek wyniesie co najmniej 5, jest równe
A) 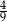 B)
B) 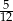 C)
C)  D)
D) 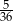
W pudełku jest 2400 kuponów, wśród których 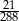 stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
A) 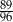 B)
B) 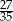 C)
C) 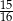 D)
D) 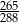
Prawdopodobieństwa zdarzeń 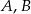 oraz zdarzeń przeciwnych
oraz zdarzeń przeciwnych 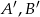 spełniają równości
spełniają równości 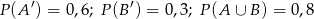 . Wtedy
. Wtedy 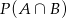 jest równe
jest równe
A) 0,5 B) 0,1 C) 0,3 D) 1
Prawdopodobieństwa zdarzeń 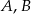 oraz zdarzeń przeciwnych
oraz zdarzeń przeciwnych 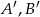 spełniają równości
spełniają równości 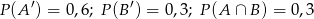 . Wtedy
. Wtedy 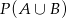 jest równe
jest równe
A) 0,6 B) 0,8 C) 0,3 D) 1
Prawdopodobieństwa zdarzeń 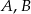 oraz zdarzeń przeciwnych
oraz zdarzeń przeciwnych 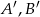 spełniają równości
spełniają równości 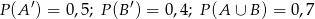 . Wtedy
. Wtedy 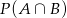 jest równe
jest równe
A) 0,4 B) 0,1 C) 0,3 D) 0,2
Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce wypadną co najmniej 4 oczka, jest równe
A) 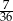 B)
B) 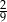 C)
C) 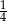 D)
D) 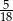
Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce wypadnie co najmniej 5 oczek, jest równe
A) 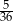 B)
B) 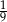 C)
C) 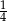 D)
D) 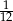
Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce wypadną co najwyżej 3 oczka, jest równe
A) 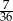 B)
B) 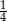 C)
C) 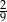 D)
D) 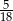
Pewnego dnia w klasie Ib było dwa razy więcej uczniów, niż w klasie Ia. Tego samego dnia dziewczynki stanowiły 60% uczniów klasy Ia, oraz 40% uczniów klasy Ib. Jeżeli tego dnia wylosujemy jednego ucznia z klas Ia i Ib, to prawdopodobieństwo wylosowania chłopca jest równe
A) 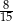 B)
B) 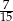 C)
C) 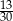 D)
D) 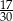
Pewnego dnia w klasie Ib było dwa razy więcej uczniów, niż w klasie Ia. Tego samego dnia dziewczynki stanowiły 40% uczniów klasy Ia, oraz 60% uczniów klasy Ib. Jeżeli tego dnia wylosujemy jednego ucznia z klas Ia i Ib, to prawdopodobieństwo wylosowania chłopca jest równe
A) 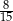 B)
B) 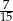 C)
C) 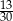 D)
D) 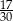
Rzucamy 10 razy symetryczną monetą. Niech 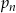 dla
dla 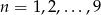 oznacza prawdopodobieństwo otrzymania dwóch orłów w rzutach o numerach
oznacza prawdopodobieństwo otrzymania dwóch orłów w rzutach o numerach  i
i 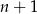 . Wtedy
. Wtedy
A) 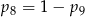 B)
B) 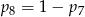 C)
C) 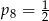 D)
D) 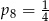
Niech 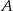 i
i 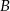 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 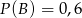 i
i 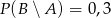 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 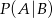 jest równe
jest równe
A) 0,3 B) 0,9 C) 0,5 D) 0,18
Niech 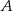 i
i 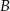 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 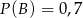 i
i 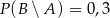 . Wtedy prawdopodobieństwo warunkowe
. Wtedy prawdopodobieństwo warunkowe 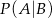 jest równe
jest równe
A) 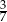 B)
B) 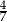 C)
C) 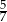 D)
D) 
Niech 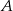 i
i 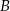 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 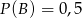 i
i 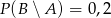 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 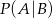 jest równe
jest równe
A) 0,3 B) 0,6 C) 0,5 D) 0,18
Z każdego ze zbiorów 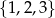 i
i 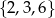 wybieramy po jednej liczbie i obliczamy ich iloczyn. Niech
wybieramy po jednej liczbie i obliczamy ich iloczyn. Niech 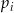 będzie prawdopodobieństwem otrzymania
będzie prawdopodobieństwem otrzymania 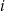 w wyniku tego działania. Wtedy
w wyniku tego działania. Wtedy
A) 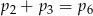 B)
B) 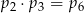 C)
C) 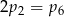 D)
D) 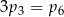
Losujemy jeden bok i jeden wierzchołek kwadratu. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowany wierzchołek jest końcem wylosowanego odcinka jest równe
A) 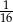 B)
B) 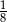 C)
C) 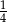 D)
D) 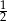
Losujemy jeden bok i jeden wierzchołek pięciokąta foremnego. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowany wierzchołek jest końcem wylosowanego odcinka jest równe
A)  B)
B) 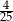 C)
C)  D)
D) 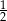
W pojemniku są wyłącznie kule białe, czerwone, niebieskie i żółte. Kul białych jest tyle samo co kul niebieskich, kul czerwonych jest dwa razy więcej niż kul żółtych, a stosunek liczby kul żółtych do liczby kul niebieskich jest równy 4 : 5. Z pojemnika losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli, która nie jest czerwona jest równe
A) 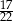 B)
B) 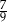 C)
C) 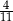 D)
D) 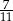
W każdym z trzech pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 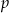 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z trzech wylosowanych kul będą czerwone. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z trzech wylosowanych kul będą czerwone. Wtedy
A) 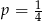 B)
B) 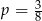 C)
C) 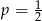 D)
D) 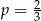
W każdym z trzech pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 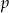 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie jedna z trzech wylosowanych kul będzie czerwona. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie jedna z trzech wylosowanych kul będzie czerwona. Wtedy
A) 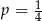 B)
B) 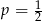 C)
C) 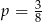 D)
D)