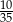Prawdopodobieństwo zdarzenia 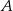 jest o 0,1 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do
jest o 0,1 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do 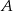 . Zatem
. Zatem 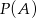 jest równe
jest równe
A) 0,6 B) 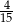 C) 0,4 D)
C) 0,4 D) 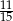
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo
Prawdopodobieństwo zdarzenia 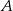 jest o 0,4 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do
jest o 0,4 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do 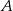 . Zatem
. Zatem 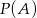 jest równe
jest równe
A) 0,6 B) 0,5 C) 0,4 D) 0,3
Dla pewnego zdarzenia losowego 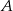 prawdziwe jest równanie (
prawdziwe jest równanie (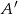 – zdarzenie przeciwne do zdarzenia
– zdarzenie przeciwne do zdarzenia 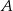 )
) 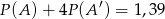 , zatem
, zatem
A) 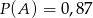 B)
B) 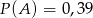 C)
C) 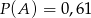 D)
D) 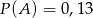
Dla pewnego zdarzenia losowego 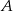 prawdziwe jest równanie (
prawdziwe jest równanie (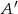 – zdarzenie przeciwne do zdarzenia
– zdarzenie przeciwne do zdarzenia 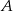 )
) 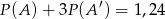 , zatem
, zatem
A) 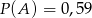 B)
B) 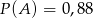 C)
C) 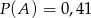 D)
D) 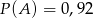
Prawdopodobieństwo, że w trzykrotnym rzucie symetryczną monetą otrzymamy dwa orły i jedną reszkę, jest równe
A)  B) 0,5 C) 0,375 D)
B) 0,5 C) 0,375 D) 
Prawdopodobieństwo, że w czterokrotnym rzucie symetryczną monetą otrzymamy trzy orły i jedną reszkę, jest równe
A)  B) 0,25 C) 0,375 D)
B) 0,25 C) 0,375 D) 
Rzucamy trzykrotnie symetryczną monetą. Prawdopodobieństwo, że w trzecim rzucie wypadnie orzeł jest równe
A) 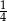 B)
B)  C)
C) 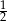 D)
D) 
Doświadczenie losowe polega na trzykrotnym rzucie monetą. Prawdopodobieństwo, że dokładnie dwa razy wylosujemy orła wynosi
A)  B)
B) 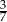 C)
C)  D)
D) 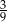
Prawdopodobieństwo, że w czterokrotnym rzucie symetryczną monetą otrzymamy trzy reszki i jednego orła, jest równe
A)  B) 0,375 C) 0,25 D)
B) 0,375 C) 0,25 D) 
Rzucamy sześć razy symetryczną sześcienną kostką do gry. Niech 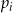 oznacza prawdopodobieństwo wyrzucenia
oznacza prawdopodobieństwo wyrzucenia 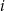 oczek w
oczek w 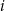 -tym rzucie. Wtedy
-tym rzucie. Wtedy
A) 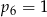 B)
B) 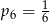 C)
C) 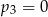 D)
D) 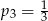
Rzucamy sześć razy symetryczną sześcienną kostką do gry. Niech 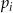 oznacza prawdopodobieństwo wyrzucenia mniej niż
oznacza prawdopodobieństwo wyrzucenia mniej niż 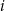 oczek w
oczek w 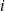 -tym rzucie. Wtedy
-tym rzucie. Wtedy
A) 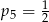 B)
B) 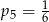 C)
C) 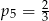 D)
D) 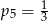
Z wierzchołków sześciokąta foremnego 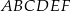 losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześciokąta
losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześciokąta 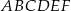 jest równe
jest równe
A)  B)
B) 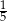 C)
C)  D)
D) 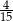
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że w zapisie dziesiętnym wylosowanej liczby jest dokładnie jedna cyfra 3?
A) 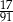 B)
B) 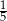 C)
C) 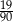 D)
D) 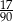
Spośród wszystkich liczb dwucyfrowych dodatnich losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 20 jest równe
A) 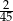 B)
B) 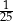 C)
C) 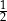 D)
D) 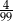
Rzucamy czterokrotnie symetryczną monetą. Prawdopodobieństwo, że otrzymamy co najmniej dwa orły jest równe
A) 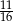 B)
B)  C)
C) 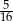 D)
D) 
Rzucamy czterokrotnie symetryczną monetą. Prawdopodobieństwo, że otrzymamy co najmniej dwie reszki jest równe
A) 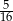 B)
B) 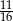 C)
C)  D)
D) 
W wycieczce szkolnej wzięło udział 12 dziewcząt i 8 chłopców z klasy Va, 13 chłopców i 11 dziewcząt z klasy Vb oraz czworo nauczycieli. Prawdopodobieństwo, że losowo wybrany uczestnik wycieczki jest chłopcem z klasy Va, jest równe
A)  B)
B) 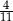 C)
C) 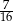 D)
D) 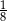
Kasia wykonała rzut trzema sześciennymi kostkami do gry i otrzymała sumę oczek większą niż 16. Prawdopodobieństwo, że Kasia wyrzuciła trzy szóstki jest równe
A) 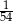 B)
B)  C)
C) 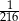 D)
D) 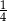
Jacek wykonał rzut trzema sześciennymi kostkami do gry i otrzymał sumę oczek mniejszą niż 5. Prawdopodobieństwo, że Jacek wyrzucił przynajmniej jedną dwójkę jest równe
A) 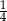 B)
B)  C)
C)  D)
D) 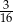
Ze zbioru cyfr 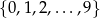 losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wybrane w kolejności losowania cyfry utworzą dwucyfrową liczbę parzystą, jest równe
losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wybrane w kolejności losowania cyfry utworzą dwucyfrową liczbę parzystą, jest równe
A) 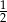 B)
B) 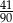 C)
C)  D)
D) 
Ze zbioru cyfr 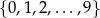 losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wyjęte w kolejności losowania cyfry utworzą liczbę nieparzystą, jest równe
losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wyjęte w kolejności losowania cyfry utworzą liczbę nieparzystą, jest równe
A)  B)
B) 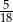 C)
C) 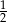 D)
D) 
Ze zbioru cyfr 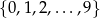 losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wylosowane cyfry (w kolejności losowania) utworzą liczbę podzielną przez 5 jest równe
losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wylosowane cyfry (w kolejności losowania) utworzą liczbę podzielną przez 5 jest równe
A) 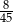 B)
B) 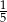 C)
C)  D)
D) 
Losujemy jeden wierzchołek i jedną ścianę sześcianu. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowany wierzchołek jest wierzchołkiem wylosowanej ściany jest równe
A) 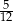 B)
B) 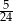 C)
C) 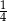 D)
D) 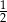
Losujemy jeden wierzchołek i jedną ścianę czworościanu foremnego. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowany wierzchołek jest wierzchołkiem wylosowanej ściany jest równe
A) 1 B) 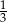 C)
C) 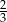 D)
D) 
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia co najmniej raz liczby oczek podzielnej przez 3 jest równe
A) 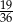 B)
B) 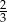 C)
C) 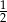 D)
D) 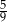
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą dwucyfrową, jest równe
A)  B)
B)  C)
C) 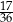 D)
D) 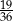
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo otrzymania co najmniej raz pięciu oczek jest równe
A) 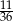 B)
B) 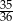 C)
C) 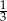 D)
D) 
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia co najmniej raz liczby oczek większej od 4 jest równe
A) 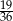 B)
B) 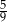 C)
C) 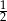 D)
D) 
Z talii 52 kart wylosowano jedną kartę. Jakie jest prawdopodobieństwo, że wylosowano pikową damę lub kierowego waleta?
A) 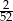 B)
B) 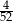 C)
C) 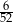 D)
D) 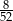
W pudełku znajdują się kule w trzech kolorach: czerwone, białe i niebieskie, przy czym prawdopodobieństwo wylosowania kuli czerwonej jest dwa razy mniejsze od prawdopodobieństwa wylosowania kuli białej, a prawdopodobieństwo wylosowania kuli niebieskiej jest trzy razy mniejsze od prawdopodobieństwa wylosowania kuli czerwonej. Prawdopodobieństwo wylosowania kuli białej jest równe
A)  B)
B)  C)
C) 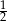 D)
D) 
Ze zbioru 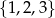 wybieramy dwie liczby (mogą się powtarzać), a ze zbioru
wybieramy dwie liczby (mogą się powtarzać), a ze zbioru 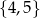 jedną liczbę. Na ile sposobów można to zrobić tak, aby otrzymane 3 liczby były długościami boków pewnego trójkąta?
jedną liczbę. Na ile sposobów można to zrobić tak, aby otrzymane 3 liczby były długościami boków pewnego trójkąta?
A) 2 B) 3 C) 4 D) 6
W pewnej szkole 20% uczniów klas trzecich pisało maturę próbną z matematyki, przy czym 90% spośród piszących otrzymało z próbnej matury więcej niż 35 punktów. Spośród wszystkich uczniów klas trzecich wybrano losowo jednego ucznia. Prawdopodobieństwo, że wybrano ucznia, który pisał maturę próbną z matematyki i otrzymał więcej niż 35 punktów jest równe
A) 0,18 B) 0,45 C) 0,9 D) 0,72
W pewnej szkole 30% uczniów klas trzecich pisało maturę próbną z matematyki, przy czym 80% spośród piszących otrzymało z próbnej matury więcej niż 35 punktów. Spośród wszystkich uczniów klas trzecich wybrano losowo jednego ucznia. Prawdopodobieństwo, że wybrano ucznia, który pisał maturę próbną z matematyki i otrzymał więcej niż 35 punktów jest równe
A) 0,8 B) 0,24 C) 0,27 D) 0,375
W pewnej szkole 40% uczniów klas trzecich pisało maturę próbną z matematyki, przy czym 80% spośród piszących otrzymało z próbnej matury więcej niż 35 punktów. Spośród wszystkich uczniów klas trzecich wybrano losowo jednego ucznia. Prawdopodobieństwo, że wybrano ucznia, który pisał maturę próbną z matematyki i otrzymał więcej niż 35 punktów jest równe
A) 0,68 B) 0,5 C) 0,32 D) 0,72
Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najmniej trzy orły, jest równe
A) 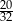 B)
B) 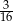 C)
C) 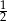 D)
D) 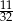
Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najwyżej 2 reszki, jest równe
A) 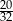 B)
B) 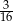 C)
C) 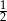 D)
D) 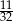
Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najmniej trzy reszki, jest równe
A) 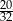 B)
B) 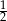 C)
C) 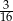 D)
D) 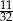
Ze zbioru liczb naturalnych dwucyfrowych nie większych niż 35 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 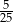 B)
B) 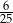 C)
C) 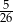 D)
D) 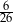
Ze zbioru liczb 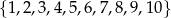 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby parzystej jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby parzystej jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Ze zbioru liczb 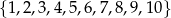 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby podzielnej przez 3 lub 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby podzielnej przez 3 lub 4 jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe
A)  B)
B) 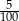 C)
C) 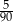 D)
D) 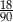
Ze zbioru kolejnych liczb naturalnych 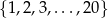 losujemy jedną liczbę. Prawdopodobieństwo, że wylosujemy liczbę podzielną przez 3 jest równe
losujemy jedną liczbę. Prawdopodobieństwo, że wylosujemy liczbę podzielną przez 3 jest równe
A) 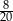 B)
B) 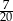 C)
C) 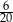 D)
D) 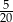
Z talii 52 kart losujemy jedną. Prawdopodobieństwo tego, że wylosujemy kartę trefl lub waleta lub króla, jest równe
A) 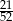 B)
B) 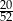 C)
C) 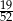 D)
D) 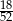
Z talii 52 kart losujemy jedną. Prawdopodobieństwo tego, że wylosujemy kartę trefl lub pik lub waleta, jest równe
A) 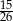 B)
B) 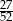 C)
C) 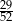 D)
D) 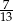
Z talii 52 kart losujemy jedną. Prawdopodobieństwo tego, że wylosujemy kartę pik lub damę lub króla, jest równe
A) 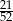 B)
B) 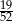 C)
C) 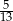 D)
D) 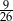
W pudełku znajdują się tylko kule białe, kule czerwone i kule zielone. Prawdopodobieństwo wylosowania z pudełka kuli zielonej jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czerwonej i dwa razy mniejsze niż wylosowanie kuli białej. Prawdopodobieństwo wylosowania z pudełka kuli zielonej jest równe
A) 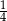 B)
B) 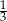 C)
C)  D)
D) 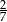
W pudełku znajdują się tylko kule białe, kule czerwone i kule zielone. Prawdopodobieństwo wylosowania z pudełka kuli czerwonej jest dwa razy większe niż prawdopodobieństwo wylosowania kuli białej i dwa razy mniejsze niż wylosowanie kuli zielonej. Prawdopodobieństwo wylosowania z pudełka kuli białej jest równe
A) 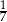 B)
B) 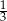 C)
C)  D)
D) 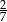
W konkursie matematycznym, w którym przewidziano tylko jedną nagrodę I stopnia, bierze udział 15 uczniów. Prawdopodobieństwo, że zwycięży Agnieszka jest równe 0,20. Prawdopodobieństwo, że zwycięży Piotrek jest równe 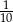 . Prawdopodobieństwo, że zwycięży Agnieszka lub Piotrek jest równe
. Prawdopodobieństwo, że zwycięży Agnieszka lub Piotrek jest równe
A) 0,02 B) 0,3 C) 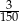 D)
D) 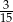
W konkursie biologicznym, w którym przewidziano tylko jedną nagrodę I stopnia, bierze udział 20 uczniów. Prawdopodobieństwo, że zwycięży Wojtek jest równe 0,30. Prawdopodobieństwo, że zwycięży Gosia jest równe 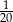 . Prawdopodobieństwo, że zwycięży Wojtek lub Gosia jest równe
. Prawdopodobieństwo, że zwycięży Wojtek lub Gosia jest równe
A) 0,25 B) 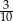 C) 0,35 D)
C) 0,35 D) 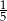
W zawodach pływackich, w których przewidziano tylko jedną nagrodę I stopnia, bierze udział 35 uczniów. Prawdopodobieństwo, że zwycięży Jola jest równe 0,10. Prawdopodobieństwo, że zwycięży Antek jest równe 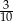 . Prawdopodobieństwo, że zwycięży Jola lub Antek jest równe
. Prawdopodobieństwo, że zwycięży Jola lub Antek jest równe
A) 0,4 B) 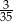 C) 0,02 D)
C) 0,02 D)