Zadanie nr 1907467
Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli niebieskiej jest równe 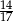 , a prawdopodobieństwo wybrania co najwyżej jednej kuli niebieskiej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli niebieskiej jest równe 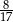 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul niebieskich jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul niebieskich jest równe
A) 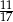 B)
B) 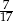 C)
C) 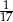 D)
D) 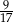
Rozwiązanie
Jeżeli oznaczymy przez 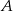 prawdopodobieństwo wylosowania co najmniej jednej kuli niebieskiej, a przez
prawdopodobieństwo wylosowania co najmniej jednej kuli niebieskiej, a przez 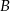 prawdopodobieństwo wylosowania co najwyżej jednej kuli niebieskiej przez
prawdopodobieństwo wylosowania co najwyżej jednej kuli niebieskiej przez  , to suma tych zdarzeń zawiera wszystkie możliwe wyniki (bo zawsze jest albo co najmniej jedna kula niebieska, albo co najwyżej jedna kula niebieska). W takim razie
, to suma tych zdarzeń zawiera wszystkie możliwe wyniki (bo zawsze jest albo co najmniej jedna kula niebieska, albo co najwyżej jedna kula niebieska). W takim razie
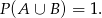
Wiemy ponadto, że 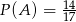 i
i 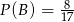 . To co mamy obliczyć to
. To co mamy obliczyć to 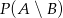 (bo jak wiemy, że jest co najmniej jedna oraz jest więcej niż jedna kula niebieska, to znaczy, że są dokładnie dwie).
(bo jak wiemy, że jest co najmniej jedna oraz jest więcej niż jedna kula niebieska, to znaczy, że są dokładnie dwie).
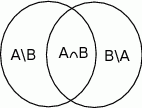
Jeżeli narysujemy diagram Venna to widać, że
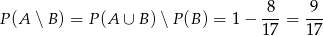
Odpowiedź: D

