Zadanie nr 8144270
Rzucamy czterokrotnie symetryczną monetą. Prawdopodobieństwo, że otrzymamy co najmniej dwa orły jest równe
A) 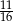 B)
B)  C)
C) 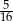 D)
D) 
Rozwiązanie
Obliczmy, ile jest zdarzeń elementarnych
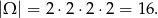
Sposób I
Wypisujemy zdarzenia sprzyjające
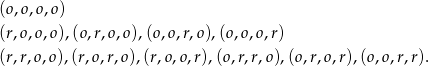
Jest więc 11 zdarzeń sprzyjających i prawdopodobieństwo jest równe 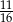 .
.
Sposób II
Zdarzeń sprzyjających jest sporo, więc łatwiej jest wypisać zdarzenia, które nie są sprzyjające, czyli takie, w których otrzymaliśmy mniej niż dwa orły:
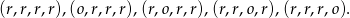
W takim razie zdarzeń sprzyjających jest 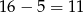 i prawdopodobieństwo jest równe
i prawdopodobieństwo jest równe  .
.
Odpowiedź: A

