Zadanie nr 8758171
Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najmniej trzy orły, jest równe
A) 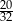 B)
B) 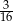 C)
C) 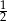 D)
D) 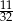
Rozwiązanie
Jeżeli o wynikach myślimy jak o piątkach wyników rzutu monetą, to
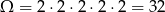
(w każdym rzucie mamy 2 możliwe wyniki).
Sposób I
Wypisujemy wszystkie możliwe zdarzenia sprzyjające
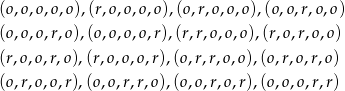
W sumie jest ich 16, czyli prawdopodobieństwo wynosi
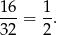
Sposób II
Zdarzenia sprzyjające są piątkami, w których orzeł wypadł co najmniej 3 razy, czyli wypadł 3,4 lub 5 razy. Liczymy ile jest wyników sprzyjających w których orzeł wypadł 3 razy (czyli liczymy na ile sposobów możemy wybrać 3 pozycje ze zbioru 5 pozycji)
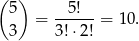
Podobnie liczymy wyniki sprzyjające w których orzeł wypadł 4 razy
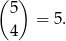
Należy również pamiętać o serii rzutów w której wypadły same orły
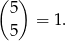
Dodajemy do siebie otrzymane wyniki i otrzymujemy szukane prawdopodobieństwo
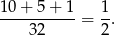
Sposób III
Niech 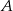 będzie zdarzeniem polegającym na otrzymaniu co najmniej trzech orłów, a
będzie zdarzeniem polegającym na otrzymaniu co najmniej trzech orłów, a 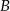 zdarzeniem polegającym na otrzymaniu co najmniej trzech reszek. Oczywiście
zdarzeniem polegającym na otrzymaniu co najmniej trzech reszek. Oczywiście 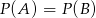 (bo monety są symetryczne). Ponadto
(bo monety są symetryczne). Ponadto 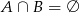 (oba warunki nie mogą być spełnione jednocześnie) oraz
(oba warunki nie mogą być spełnione jednocześnie) oraz 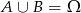 (zawsze są albo co najmniej trzy orły, albo co najmniej trzy reszki). W takim razie
(zawsze są albo co najmniej trzy orły, albo co najmniej trzy reszki). W takim razie
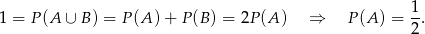
Odpowiedź: C

