Zadanie nr 9179817
Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najwyżej 2 reszki, jest równe
A) 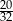 B)
B) 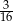 C)
C) 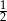 D)
D) 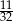
Rozwiązanie
Jeżeli o wynikach myślimy jak o piątkach wyników rzutu monetą, to
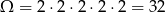
(w każdym rzucie mamy 2 możliwe wyniki).
Sposób I
Wypisujemy wszystkie możliwe zdarzenia sprzyjające

W sumie jest ich 16, czyli prawdopodobieństwo wynosi
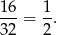
Sposób II
Zdarzenia sprzyjające są piątkami, w których reszka wypadła co najwyżej 2 razy, czyli wypadła 0,1 lub 2 razy. Liczymy ile jest wyników sprzyjających, w których reszka wypadła 2 razy (czyli liczymy na ile sposobów możemy wybrać 2 pozycje ze zbioru 5 pozycji)
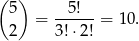
Podobnie liczymy wyniki sprzyjające, w których reszka wypadła 1 raz
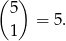
Należy również pamiętać o serii rzutów w której wypadły same orły
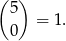
Dodajemy do siebie otrzymane wyniki i otrzymujemy szukane prawdopodobieństwo
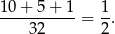
Odpowiedź: C

