Zestaw użytkownika nr 1095_9540
Zestaw użytkownika
nr 1095_9540
Uprość wyrażenie 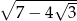 .
.
Uzasadnij, że dla każdej liczby 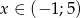 wyrażenie
wyrażenie 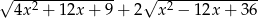 ma stałą wartość.
ma stałą wartość.
Oblicz 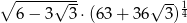 .
.
Dany ciąg arytmetyczny 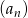 taki, że
taki, że 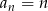 , dla
, dla 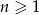 . Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez
. Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez 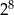 .
.
Uzasadnij, że liczby 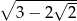 i
i 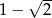 są liczbami przeciwnymi.
są liczbami przeciwnymi.
Wykaż, że dla 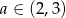 zachodzi równość
zachodzi równość 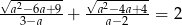 .
.
Uzasadnij, że jeżeli  jest liczbą całkowitą to liczba
jest liczbą całkowitą to liczba 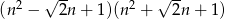 też jest liczbą całkowitą.
też jest liczbą całkowitą.
Wiadomo, że 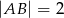 i
i 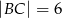 . Znajdź warunek, jaki musi spełniać odległość
. Znajdź warunek, jaki musi spełniać odległość 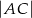 , aby punkty
, aby punkty 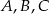 były współliniowe.
były współliniowe.
Udowodnij, że iloczyn kolejnych liczb naturalnych od 1 do 16, czyli 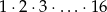 , jest podzielny przez
, jest podzielny przez 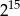 .
.
Wiedząc, że liczba  jest rozwiązaniem równania
jest rozwiązaniem równania 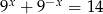 , wyznacz wartość wyrażenia
, wyznacz wartość wyrażenia 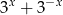 .
.
Wiadomo, że 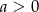 i
i 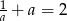 . Wykaż, że
. Wykaż, że 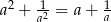 .
.
Udowodnij, że jeśli 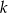 i
i  są liczbami naturalnymi oraz
są liczbami naturalnymi oraz 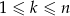 , to
, to 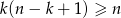 .
.
Udowodnij, że dla każdej liczby naturalnej  , liczba
, liczba 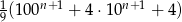 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Udowodnij, że liczby 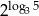 i
i 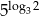 są równe.
są równe.
Uzasadnij, że jeśli 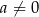 oraz
oraz 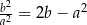 , to
, to 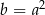 .
.
Wykaż, że 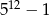 jest liczbą podzielną przez 31.
jest liczbą podzielną przez 31.
Porównaj liczby 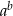 i
i 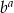 , gdzie
, gdzie ![[ √ --1 √ --1]2 a = (2− 3)2 + (2+ 3)2](https://img.zadania.info/zad/6242955/HzadT2x.gif) ,
, 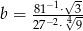 .
.
Wykaż, że liczba  jest dla dowolnej liczby naturalnej
jest dla dowolnej liczby naturalnej  kwadratem liczby całkowitej.
kwadratem liczby całkowitej.
Uzasadnij, że jeśli 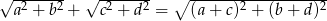 to
to 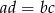 .
.

