Zadanie nr 1379457
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 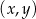 , dana jest prosta
, dana jest prosta 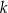 o równaniu
o równaniu 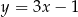 . Jedną z prostych prostopadłych do prostej
. Jedną z prostych prostopadłych do prostej 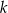 jest prosta o równaniu
jest prosta o równaniu
A) 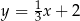 B)
B) 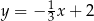 C)
C) 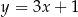 D)
D) 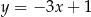
Rozwiązanie
Proste 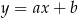 i
i 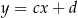 są prostopadłe jeżeli
są prostopadłe jeżeli 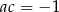 . Podana prosta ma współczynnik kierunkowy równy 3, czyli prostą prostopadłą do niej jest prosta
. Podana prosta ma współczynnik kierunkowy równy 3, czyli prostą prostopadłą do niej jest prosta 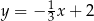 .
.
Odpowiedź: B

