Zestaw użytkownika nr 1133_2744
Zestaw użytkownika
nr 1133_2744
Rozwiąż nierówność 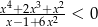 .
.
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 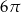 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 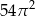 B)
B) 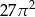 C)
C) 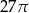 D)
D) 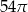
Na rysunku przedstawiony jest wykres funkcji 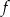 określonej wzorem
określonej wzorem 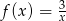 dla
dla 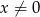 .
.
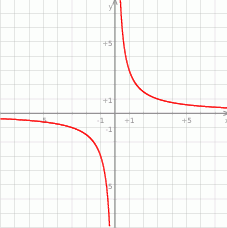
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 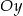 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 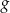 o wzorze
o wzorze 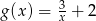 dla
dla 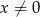 .
.
- Narysuj wykres funkcji
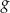 .
. - Oblicz największą wartość funkcji
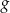 w przedziale
w przedziale 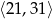 .
. - Podaj, o ile jednostek wzdłuż osi
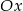 należy przesunąć wykres funkcji
należy przesunąć wykres funkcji 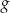 , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
Rozwiązaniem równania 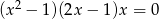 nie jest liczba
nie jest liczba
A) 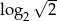 B)
B) 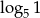 C)
C) 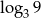 D)
D) 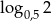
Wyrażenie 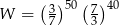 jest równe
jest równe
A) 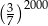 B)
B) 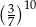 C)
C) 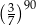 D) 1
D) 1
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 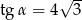 oblicz wartość wyrażenia
oblicz wartość wyrażenia 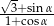 .
.
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia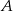 – na każdej kostce wypadła nieparzysta liczba oczek,
– na każdej kostce wypadła nieparzysta liczba oczek,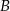 – suma wyrzuconych oczek jest nie mniejsza niż 8.
– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 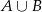 .
.
Suma kolejnych liczb nieparzystych mniejszych od 100 jest równa
A) 5050 B) 2450 C) 2525 D) 2500
Rosnące, trzywyrazowe ciągi arytmetyczny i geometryczny mają pierwsze wyrazy równe 9. Trzecie wyrazy tych ciągów są także równe. Drugi wyraz ciągu arytmetycznego jest o 2 większy od drugiego wyrazu ciągu geometrycznego. Wyznacz te ciągi.
Wielomian 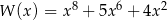 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) wartości niedodatnie
B) wartości nieujemne
C) tylko wartości ujemne
D) tylko wartości dodatnie
Dla jakich wartości parametru 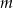 równanie
równanie 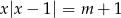 ma dwa różne rozwiązania?
ma dwa różne rozwiązania?
Wykres funkcji homograficznej 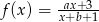 można otrzymać przesuwając wykres funkcji
można otrzymać przesuwając wykres funkcji 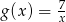 , a dziedzina funkcji
, a dziedzina funkcji 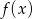 jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki
jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki  i
i 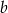 .
.

