Zestaw użytkownika nr 1153_4507
Zestaw użytkownika
nr 1153_4507
Zadanie 1
Liczby 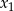 i
i 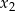 są różnymi miejscami zerowymi funkcji kwadratowej
są różnymi miejscami zerowymi funkcji kwadratowej 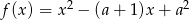 . Dla jakich
. Dla jakich  ciąg
ciąg 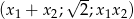 jest geometryczny?
jest geometryczny?
Zadanie 2
Współczynniki 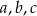 równania
równania 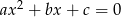 są kolejnymi wyrazami ciągu arytmetycznego, a ich suma wynosi 24. Jednym z rozwiązań równania jest liczba
są kolejnymi wyrazami ciągu arytmetycznego, a ich suma wynosi 24. Jednym z rozwiązań równania jest liczba 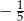 Wyznacz
Wyznacz 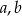 i
i  .
.
Zadanie 3
Dany jest ciąg arytmetyczny 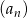 , gdzie
, gdzie 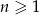 . Wiadomo, że dla każdego
. Wiadomo, że dla każdego 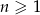 suma
suma  początkowych wyrazów
początkowych wyrazów 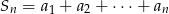 wyraża się wzorem:
wyraża się wzorem: 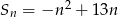 .
.
- Wyznacz wzór na
 –ty wyraz ciągu
–ty wyraz ciągu 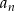 .
. - Oblicz
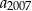 .
. - Wyznacz liczbę
 , dla której
, dla której 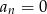 . .
. .
Zadanie 4
Nieskończony ciąg liczbowy 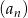 określony jest wzorem:
określony jest wzorem:
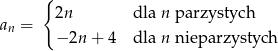
- Wyznacz sumę dwudziestu początkowych wyrazów ciągu.
- Zbadaj, czy istnieje wyraz ciągu równy 5. Odpowiedź uzasadnij.
Zadanie 5
Ciąg 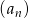 określony jest rekurencyjnie:
określony jest rekurencyjnie: 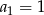 ,
, 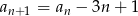 dla
dla 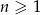 .
.
- Oblicz 4 wyraz ciągu
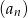 .
. - Zbadaj monotoniczność ciągu
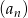 .
.
Zadanie 6
Podaj wzór na  -ty wyraz ciągu
-ty wyraz ciągu 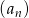 , jeżeli
, jeżeli 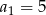 i
i 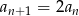 dla
dla 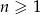 .
.
Zadanie 7
Wyznacz drugi, trzeci i czwarty wyraz ciągu określonego wzorem rekurencyjnym:
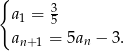
Dla wyznaczonych wyrazów znajdź taką liczbę  , aby ciąg
, aby ciąg 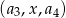 był ciągiem geometrycznym.
był ciągiem geometrycznym.

