Zestaw użytkownika nr 1157_3850
Zestaw użytkownika
nr 1157_3850
Napisz równanie okręgu, którego środek należy do osi 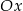 , i który przechodzi przez punkty
, i który przechodzi przez punkty 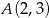 i
i 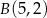 .
.
W układzie współrzędnych dane są dwa punkty: 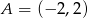 i
i 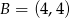 .
.
- Wyznacz równanie symetralnej odcinka
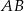 .
. - Prosta
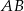 oraz prosta o równaniu
oraz prosta o równaniu 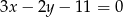 przecinają się w punkcie
przecinają się w punkcie 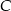 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 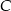 .
.
Punkty 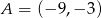 i
i 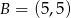 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 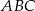 , w którym
, w którym 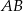 jest przeciwprostokątną. Wyznacz współrzędne wierzchołka
jest przeciwprostokątną. Wyznacz współrzędne wierzchołka 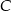 wiedząc, że leży on na osi
wiedząc, że leży on na osi 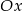 .
.
Dane są dwa przeciwległe wierzchołki kwadratu 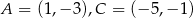 . Wyznacz obwód tego kwadratu.
. Wyznacz obwód tego kwadratu.
Dany jest jeden koniec odcinka 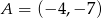 i jego środek
i jego środek 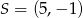 . Wyznacz współrzędne drugiego końca tego odcinka.
. Wyznacz współrzędne drugiego końca tego odcinka.
Współrzędne przeciwległych wierzchołków prostokąta 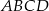 są równe
są równe 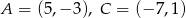 . Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek
. Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek 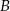 leży na prostej
leży na prostej 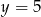 .
.
Punkty 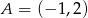 i
i 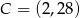 są wierzchołkami trójkąta równoramiennego, w którym
są wierzchołkami trójkąta równoramiennego, w którym 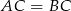 . Prosta zawierająca wysokość opuszczoną z wierzchołka
. Prosta zawierająca wysokość opuszczoną z wierzchołka 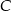 ma równanie
ma równanie 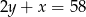 . Oblicz pole trójkąta
. Oblicz pole trójkąta 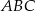 .
.
Podstawa 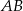 trójkąta równobocznego
trójkąta równobocznego 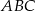 zawarta jest w prostej
zawarta jest w prostej 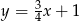 , a wierzchołek
, a wierzchołek 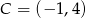 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 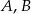 tego trójkąta.
tego trójkąta.
Napisz równanie okręgu o środku w punkcie 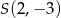 , stycznego do osi
, stycznego do osi 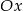 .
.
Wyznacz równanie prostej, która przecina oś 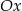 pod kątem
pod kątem 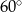 , a oś
, a oś 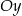 w punkcie
w punkcie 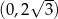 .
.
W kwadracie 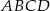 dane są wierzchołek
dane są wierzchołek 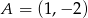 i środek symetrii
i środek symetrii 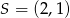 . Oblicz pole kwadratu
. Oblicz pole kwadratu 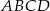 .
.
Napisz równanie prostej równoległej do prostej o równaniu 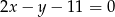 i przechodzącej przez punkt
i przechodzącej przez punkt 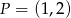 .
.
Wyznacz współrzędne punktów wspólnych prostej 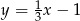 i okręgu
i okręgu 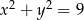 .
.
Punkt 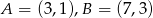 są kolejnymi wierzchołkami kwadratu
są kolejnymi wierzchołkami kwadratu 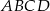 . Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.
. Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.
Zapisz równanie prostej przechodzącej przez punkt 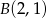 i prostopadłej do prostej danej równaniem
i prostopadłej do prostej danej równaniem 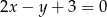 .
.
Wyznacz równanie okręgu wpisanego w kwadrat 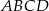 , gdzie
, gdzie 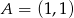 i
i 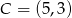 .
.
W okrąg o równaniu 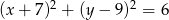 wpisano kwadrat. Oblicz pole tego kwadratu.
wpisano kwadrat. Oblicz pole tego kwadratu.
Dany jest okrąg o równaniu 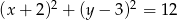 oraz punkt
oraz punkt 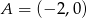 . Napisz równanie symetralnej odcinka, którego końcami są dany punkt
. Napisz równanie symetralnej odcinka, którego końcami są dany punkt 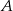 i środek
i środek 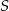 danego okręgu.
danego okręgu.
Dany jest trójkąt 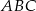 o wierzchołkach
o wierzchołkach 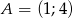 ,
, 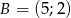 ,
, 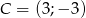 .
.
- Napisz równanie wysokości opuszczonej z wierzchołka
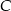 na bok
na bok 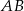 .
. - Napisz równanie środkowej boku
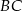 .
. - Napisz równanie symetralnej boku
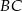 .
. - Oblicz obwód i pole tego trójkąta.
Wykaż, że trójkąt 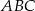 o wierzchołkach
o wierzchołkach 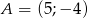 ,
, 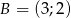 ,
, 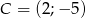 jest prostokątny.
jest prostokątny.

