Zestaw użytkownika nr 1210_4061
Funkcja kwadratowaPoziom podstawowy9 Czerwca 2012Czas pracy: 40 min.Suma punktów: 20
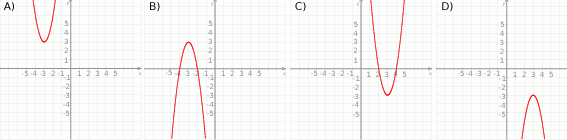
Na rysunku jest przedstawiony wykres funkcji 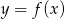 .
.
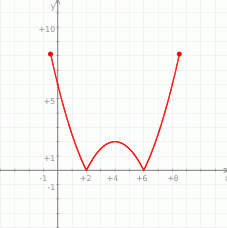
Które równanie ma dokładnie trzy rozwiązania?
A) 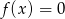 B)
B) 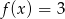 C)
C) 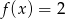 D)
D) 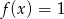
Zbiorem wartości funkcji kwadratowej 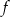 jest przedział
jest przedział 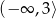 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 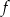 ?
?
Zbiór wartości funkcji kwadratowej 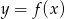 jest rozłączny z przedziałem
jest rozłączny z przedziałem 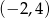 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji  ?
?
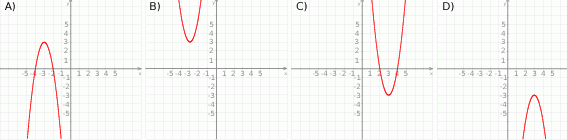
Wskaż funkcję, która nie przyjmuje wartości ujemnych
A) 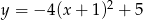 B)
B) 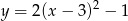 C)
C) 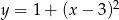 D)
D) 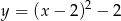
Największą wartością funkcji kwadratowej 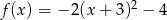 jest
jest
A) 3 B) -4 C) -2 D) 4
Zbiorem wartości funkcji kwadratowej 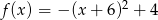 jest przedział
jest przedział
A) 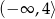 B)
B) 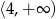 C)
C) 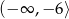 D)
D) 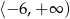
Sprowadź do postaci ogólnej funkcję kwadratową 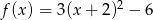 .
.
Wyznacz najmniejszą i największą wartość funkcji 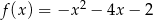 w przedziale
w przedziale 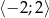 .
.
Określ zbiór wartości funkcji: 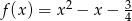 . Dla jakich argumentów funkcja przyjmuje wartości ujemne?
. Dla jakich argumentów funkcja przyjmuje wartości ujemne?
Funkcja kwadratowa 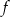 przyjmuje największą wartość równą
przyjmuje największą wartość równą 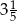 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 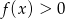 jest przedział
jest przedział 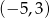 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 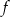 w postaci ogólnej.
w postaci ogólnej.

