Zestaw użytkownika nr 1278_7927
WielomianySuma punktów: 125
Reszta z dzielenia wielomianu 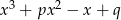 przez trójmian
przez trójmian 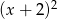 wynosi
wynosi 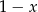 . Wyznacz pierwiastki tego wielomianu.
. Wyznacz pierwiastki tego wielomianu.
Wielomian 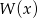 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 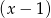 ,
, 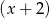 ,
, 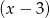 daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian
daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 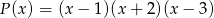 .
.
Reszta z dzielenia wielomianu 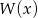 przez wielomian
przez wielomian 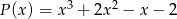 jest równa
jest równa 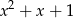 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 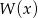 przez wielomian
przez wielomian 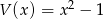 .
.
Dane są wielomiany 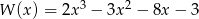 i
i 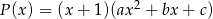 .
.
- Wyznacz współczynniki
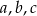 tak, aby
tak, aby 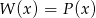 .
. - Przedstaw wielomian
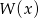 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych.
Dany jest wielomian 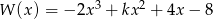 .
.
- Wyznacz wartość
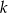 tak, aby reszta z dzielenia wielomianu W przez dwumian
tak, aby reszta z dzielenia wielomianu W przez dwumian 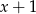 była równa -6.
była równa -6. - Dla znalezionej wartości
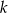 rozłóż wielomian na czynniki liniowe.
rozłóż wielomian na czynniki liniowe. - Dla znalezionej wartości
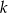 rozwiąż nierówność
rozwiąż nierówność 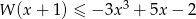 .
.
Wyznacz współczynniki 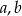 wielomianu
wielomianu 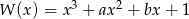 wiedząc, że dla każdego
wiedząc, że dla każdego 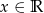 prawdziwa jest równość:
prawdziwa jest równość: 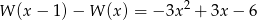 .
.
Wielomian 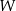 jest wielomianem stopnia 5 i spełnia warunki:
jest wielomianem stopnia 5 i spełnia warunki: 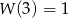 oraz
oraz 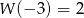 . Wykaż, że nie wszystkie współczynniki wielomianu
. Wykaż, że nie wszystkie współczynniki wielomianu 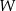 są liczbami całkowitymi.
są liczbami całkowitymi.
Wielomian 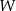 dany jest wzorem
dany jest wzorem 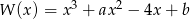 .
.
- Wyznacz
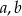 oraz
oraz  tak, aby wielomian
tak, aby wielomian 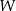 był równy wielomianowi
był równy wielomianowi 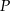 , gdy
, gdy 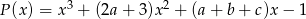 .
. - Dla
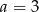 i
i 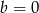 zapisz wielomian
zapisz wielomian 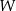 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Dla jakich wartości parametru  , wielomian
, wielomian 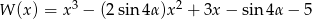 jest podzielny przez dwumian
jest podzielny przez dwumian 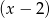 ?
?
Rozłóż wielomian 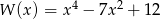 na czynniki liniowe. Podaj niewymierne pierwiastki tego wielomianu.
na czynniki liniowe. Podaj niewymierne pierwiastki tego wielomianu.
Rozłóż wielomian 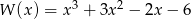 na czynniki liniowe.
na czynniki liniowe.
Dla jakich wartości parametru 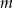 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu
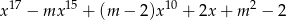
przez dwumian 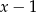 jest równa 3?
jest równa 3?
Wielomian 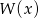 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 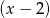 ,
, 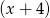 daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu
daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu 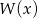 przez wielomian
przez wielomian 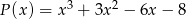 , wiedząc, że liczba -1 jest miejscem zerowym wielomianu
, wiedząc, że liczba -1 jest miejscem zerowym wielomianu 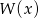 .
.
Wielomian 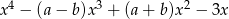 jest podzielny przez wielomian
jest podzielny przez wielomian 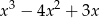 . Oblicz
. Oblicz  i
i 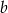 .
.
Przy dzieleniu wielomianu 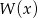 przez dwumian
przez dwumian 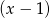 otrzymujemy iloraz
otrzymujemy iloraz 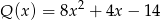 oraz resztę
oraz resztę 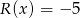 . Oblicz pierwiastki wielomianu
. Oblicz pierwiastki wielomianu 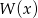 .
.
Wyznacz te argumenty, dla których funkcja 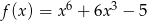 osiąga wartość najmniejszą.
osiąga wartość najmniejszą.
Reszta z dzielenia wielomianu 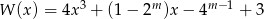 przez dwumian
przez dwumian 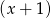 jest równa -2.
jest równa -2.
- Wyznacz wartość parametru
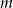 .
. - Dla wyznaczonej wartości parametru
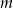 rozwiąż nierówność
rozwiąż nierówność 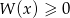 .
.
Wielomian 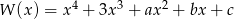 jest podzielny przez trójmian
jest podzielny przez trójmian 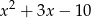 , a przy dzieleniu przez dwumian
, a przy dzieleniu przez dwumian 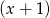 daje resztę -36. Wyznacz współczynniki
daje resztę -36. Wyznacz współczynniki 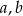 i
i  wielomianu.
wielomianu.
Korzystając z definicji funkcji rożnowartościowej wykaż, że funkcja 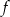 określona wzorem
określona wzorem 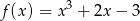 jest rożnowartościowa.
jest rożnowartościowa.
Wyznacz zbiór wartości funkcji 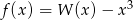 , gdzie
, gdzie 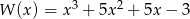 .
.
Wiedząc, że wielomian 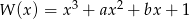 jest podzielny przez wielomian
jest podzielny przez wielomian 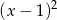 , oblicz
, oblicz  i
i 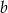 .
.
Reszta z dzielenia wielomianu 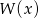 przez wielomian
przez wielomian 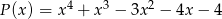 jest wielomianem
jest wielomianem 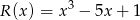 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 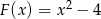 .
.
Dany jest wielomian 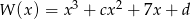 .
.
- Wyznacz wartości współczynników
 i
i 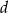 wielomianu
wielomianu 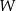 , wiedząc, że jest podzielny przez dwumian
, wiedząc, że jest podzielny przez dwumian 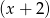 , zaś przy dzieleniu przez dwumian
, zaś przy dzieleniu przez dwumian 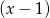 otrzymujemy resztę 3.
otrzymujemy resztę 3. - Dla
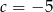 i
i 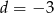 rozwiąż nierówność
rozwiąż nierówność 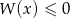 .
.
Dla jakich wartości parametru  reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 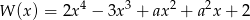 przez dwumian
przez dwumian 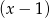 jest większa od 3.
jest większa od 3.
Wyznacz wartości  i
i 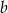 współczynników wielomianu
współczynników wielomianu 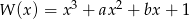 wiedząc, że
wiedząc, że 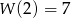 oraz, że reszta z dzielenia
oraz, że reszta z dzielenia 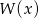 przez
przez 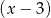 jest równa 10.
jest równa 10.

