Zestaw użytkownika nr 1292_4200
Zestaw użytkownika
nr 1292_4200
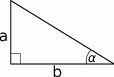
Dany jest trójkąt prostokątny o kącie ostrym 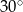 . Oblicz obwód tego trójkąta, jeżeli przeciwprostokątna ma długość 12 dm.
. Oblicz obwód tego trójkąta, jeżeli przeciwprostokątna ma długość 12 dm.
Dany jest trójkąt prostokątny, w którym  ,
, 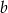 oznaczają długości przyprostokątnych,
oznaczają długości przyprostokątnych,  jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej
jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej  . Wiadomo, że
. Wiadomo, że 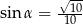 . Oblicz
. Oblicz
- tangens kąta
 ;
; - wartość wyrażenia
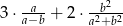 .
.
W trójkącie równobocznym 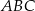 obrano na boku
obrano na boku 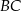 taki punkt
taki punkt 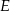 , że
, że 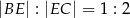 . Oblicz tangens kąta
. Oblicz tangens kąta 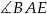 .
.
W trójkącie równoramiennym 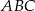 , w którym
, w którym 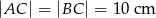 , wysokość poprowadzona z wierzchołka
, wysokość poprowadzona z wierzchołka 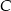 jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
Jeden z kątów trójkąta prostokątnego ma miarę 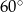 , promień okręgu wpisanego w ten trójkąt ma długość 1. Oblicz długości boków trójkąta.
, promień okręgu wpisanego w ten trójkąt ma długość 1. Oblicz długości boków trójkąta.
Miara jednego z kątów ostrych w trójkącie prostokątnym jest równa  .
.
- Uzasadnij, że spełniona jest nierówność
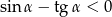 .
. - Dla
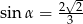 oblicz wartość wyrażenia
oblicz wartość wyrażenia 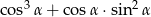 .
.
Korzystając z danych przedstawionych na rysunku oblicz wartość wyrażenia
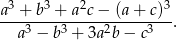
W trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 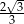 . Wykaż, że iloczyn sinusów tych kątów jest równy
. Wykaż, że iloczyn sinusów tych kątów jest równy 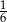 .
.
Dany jest trójkąt prostokątny 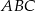 o przeciwprostokątnej
o przeciwprostokątnej 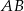 , taki że
, taki że 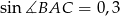 i
i 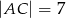 . Oblicz pole koła opisanego na tym trójkącie.
. Oblicz pole koła opisanego na tym trójkącie.
W pewnym trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 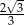 . Oblicz iloczyn sinusów tych kątów.
. Oblicz iloczyn sinusów tych kątów.
Wyznacz długości boków oraz miary kątów trójkąta prostokątnego jeżeli 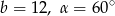 .
.
Wykaż, że jeśli 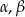 są kątami ostrymi trójkąta prostokątnego, to
są kątami ostrymi trójkąta prostokątnego, to 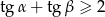 .
.
W trójkącie prostokątnym iloczyn sinusa jednego z kątów ostrych i tangensa drugiego kąta ostrego jest równy 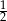 . Oblicz miary kątów ostrych tego trójkąta.
. Oblicz miary kątów ostrych tego trójkąta.
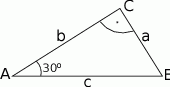
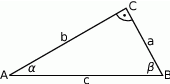
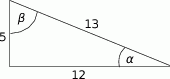
Na rysunku oznaczono kąty oraz podano długości boków trójkąta prostokątnego. Oblicz, które z wyrażeń ma większą wartość: 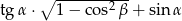 czy
czy 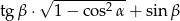 .
.
Wysokość 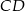 trójkąta
trójkąta 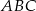 ma długość 6cm i dzieli bok
ma długość 6cm i dzieli bok 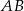 na odcinki o długościach
na odcinki o długościach 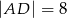 i
i 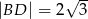 .
.
- Oblicz tangens i cosinus kąta
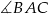 .
. - Znajdź miarę kąta
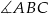 .
.
Oblicz długości boków trójkąta prostokątnego 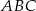 (
(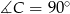 ) jeżeli
) jeżeli 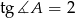 i
i 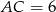 .
.
Wyznacz długości boków trójkąta prostokątnego, w którym długość przyprostokątnej wynosi 12 cm, a kąt do niej przyległy ma miarę 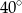 . Wynik podaj z dokładnością do 0,1 cm.
. Wynik podaj z dokładnością do 0,1 cm.
Podstawa trójkąta równoramiennego ma miarę 4 cm, a kąt przy niej 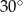 . Oblicz pole i obwód trójkąta.
. Oblicz pole i obwód trójkąta.
Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 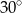 i
i 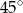 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
Dany jest trapez prostokątny 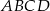 , gdzie
, gdzie 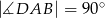 ,
, 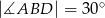 ,
, 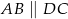 ,
, 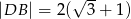 i
i 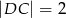 .
.
- Oblicz długość promienia okręgu wpisanego w trójkąt
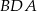 .
. - Wyznacz sumę kwadratów sinusów kątów wewnętrznych trapezu
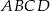 .
.
Krótsza podstawa trapezu ma długość 2, a ramiona długości 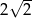 i 4 tworzą z dłuższą podstawą kąty o miarach
i 4 tworzą z dłuższą podstawą kąty o miarach 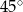 i
i 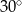 . Oblicz pole trapezu.
. Oblicz pole trapezu.
Dany jest trapez prostokątny (zobacz rysunek).
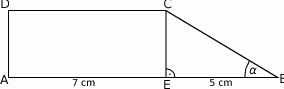
Wyznacz obwód tego trapezu, jeżeli miara kąta przy wierzchołku 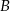 wynosi
wynosi 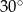 .
.
Wysokość trapezu równoramiennego ma długość 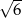 , a jedna z podstaw jest trzy razy dłuższa od drugiej. Oblicz pole trapezu wiedząc, że sinus jego kąta ostrego jest równy 0,2.
, a jedna z podstaw jest trzy razy dłuższa od drugiej. Oblicz pole trapezu wiedząc, że sinus jego kąta ostrego jest równy 0,2.

