Zestaw użytkownika nr 1352_3201
TrygonometriaSuma punktów: 91
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 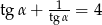 oblicz
oblicz 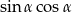 .
.
Kąt  jest kątem ostrym. Wiedząc, że
jest kątem ostrym. Wiedząc, że 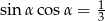 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 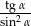 .
.
Uzasadnij, że jeżeli 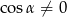 to prawdą jest, że
to prawdą jest, że 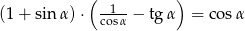 .
.
Sprawdź, czy prawdziwa jest następująca tożsamość 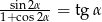 . Podaj konieczne założenia.
. Podaj konieczne założenia.
Wykaż, że nie istnieje kąt  , taki, że
, taki, że 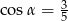 i
i 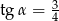 .
.
Wyznacz zbiór wartości funkcji 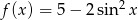 dla
dla 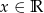 .
.
Dana jest funkcja 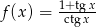 dla
dla 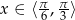 .
.
- Rozwiąż równanie
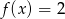 .
. - Wyznacz najmniejszą wartość funkcji
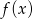 .
.
Dana jest funkcja 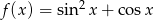 dla
dla 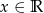 .
.
- Rozwiąż równanie
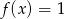 w przedziale
w przedziale 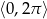 .
. - Wyznacz największą wartość funkcji
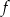 .
.
Rozwiąż równanie 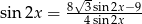 , gdzie
, gdzie 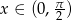 .
.
Rozwiąż równanie 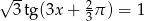 .
.
Rozwiąż równanie 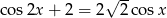 .
.
Dane jest równanie 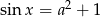 , z niewiadomą
, z niewiadomą  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których dane równanie nie ma rozwiązań.
, dla których dane równanie nie ma rozwiązań.
Rozwiąż równanie 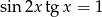 .
.
Oblicz sumę wszystkich miejsc zerowych funkcji 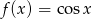 należących do przedziału
należących do przedziału 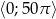 .
.
Rozwiąż nierówność 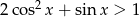 , gdzie
, gdzie 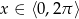 .
.
Kąt  jest ostry oraz
jest ostry oraz 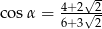 . Wtedy
. Wtedy 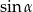 jest równy
jest równy
A) 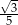 B)
B) 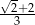 C)
C) 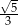 D)
D) 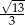
Wiadomo, że tangens kąta ostrego  jest równy
jest równy  . Wobec tego:
. Wobec tego:
A) 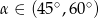 B)
B) 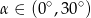 C)
C) 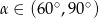 D)
D) 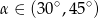
Kąt  jest kątem ostrym i
jest kątem ostrym i 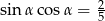 . Wówczas wyrażenie
. Wówczas wyrażenie 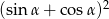 jest równe
jest równe
A) 1 B) 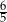 C)
C)  D)
D) 
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 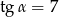 . Wówczas wartość wyrażenia
. Wówczas wartość wyrażenia 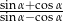 jest równa
jest równa
A)  B)
B)  C)
C)  D)
D) 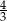
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 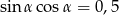 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 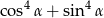 jest równa
jest równa
A) 0,25 B) 0,75 C) 1 D) 0,5
Nieprawdą jest, że
A) 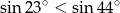 B)
B) 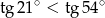 C)
C) 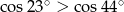 D)
D) 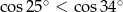
Kąt  jest kątem ostrym. Zatem liczba
jest kątem ostrym. Zatem liczba 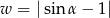 spełnia warunek
spełnia warunek
A) 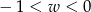 B)
B) 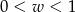 C)
C) 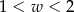 D)
D) 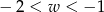
Wartość wyrażenia 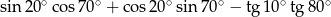 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba 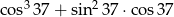 jest równa
jest równa
A) 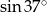 B)
B) 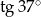 C)
C) 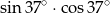 D)
D) 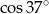
Jeżeli 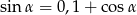 to liczba
to liczba 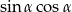 jest równa
jest równa
A) 0,99 B) 0,5 C) 0,495 D) 0,45
Wartość wyrażenia 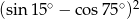 jest liczbą
jest liczbą
A) parzystą B) pierwszą C) wymierną z przedziału 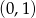 D) niewymierną
D) niewymierną
Która z liczb jest największa?
A) 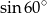 B)
B) 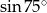 C)
C) 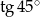 D)
D) 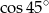
Wartość wyrażenia 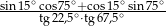 jest równa
jest równa
A) 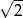 B)
B) 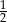 C) 1 D)
C) 1 D) 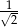
Kąt ostry  jest większy od kąta ostrego
jest większy od kąta ostrego 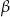 . Wynika stąd, że
. Wynika stąd, że
A) 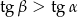 B)
B) 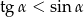 C)
C) 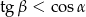 D)
D) 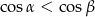
Jeśli  jest kątem ostrym i
jest kątem ostrym i  , to suma
, to suma 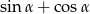 jest równa
jest równa
A) 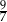 B)
B) 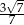 C)
C) 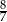 D)
D) 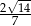
Wartość wyrażenia 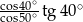 wynosi
wynosi
A) 1 B) 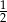 C)
C) 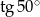 D)
D)