Zestaw użytkownika nr 1360_8990
Liczby rzeczywistepoziom rozszerzony gr. I5 Października 2011Czas pracy: 45 min.Suma punktów: 76
Wyrażenie 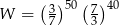 jest równe
jest równe
A) 1 B) 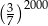 C)
C) 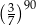 D)
D) 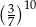
Wykaż, że jeżeli 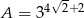 i
i 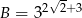 , to
, to 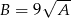 .
.
Uprość wyrażenie 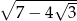 .
.
Oblicz 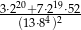 .
.
Uprość wyrażenie
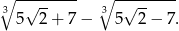
Uzasadnij, że dla każdej liczby 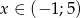 wyrażenie
wyrażenie 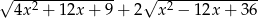 ma stałą wartość.
ma stałą wartość.
Suma dwóch liczb jest równa 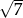 , a ich różnica
, a ich różnica 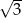 . Oblicz iloczyn tych liczb.
. Oblicz iloczyn tych liczb.
Wykaż, że jeżeli liczby całkowite 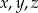 spełniają równanie
spełniają równanie 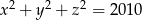 to co najwyżej jedna z liczb
to co najwyżej jedna z liczb 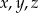 dzieli się przez 4.
dzieli się przez 4.
Wykaż, że różnica kwadratów dwóch kolejnych liczb parzystych jest liczbą podzielną przez 4.
Oblicz 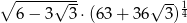 .
.
Uzasadnij, że liczby 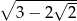 i
i 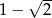 są liczbami przeciwnymi.
są liczbami przeciwnymi.
Wykaż, że liczba 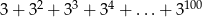 jest podzielna przez 6.
jest podzielna przez 6.
Zbiór 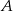 jest zbiorem liczb rzeczywistych, których odległość na osi liczbowej od (-3) jest większa niż 2. Zbiór
jest zbiorem liczb rzeczywistych, których odległość na osi liczbowej od (-3) jest większa niż 2. Zbiór 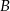 jest przedstawiony na osi liczbowej.
jest przedstawiony na osi liczbowej.
![]()
- Opisz zbiory
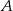 i
i 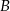 za pomocą nierówności z wartością bezwzględną.
za pomocą nierówności z wartością bezwzględną. - Podaj przykład liczby niewymiernej, która należy jednocześnie do zbioru
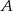 i do zbioru
i do zbioru 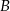 .
.
Dane są 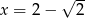 i
i 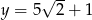 . Oblicz
. Oblicz 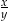 .
.
Wykaż, że liczba 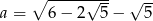 jest całkowita.
jest całkowita.
W zbiorze liczb rzeczywistych określono działanie 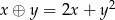 .
.
- Oblicz
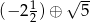
- Sprawdź, dla jakich liczb całkowitych nieujemnych
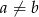 prawdziwa jest równość
prawdziwa jest równość 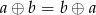 .
.

