Zestaw użytkownika nr 1409_1402

Zestaw użytkownika
nr 1409_1402

Zadanie 1

(3 pkt)

Wiedząc, że zbiorem wartości funkcji 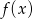f(x) jest przedział 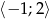⟨− 1;2⟩ wyznacz wszystkie wartości 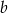, dla których funkcja 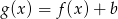g(x) = f (x)+ b nie ma miejsc zerowych.

Zadanie 2

(4 pkt)

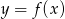Liczba jest jedynym miejscem zerowym funkcji y = f(x) . Wyznacz miejsca zerowe funkcji: y = f(x − 3) .

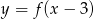Zadanie 3

(5 pkt)

Funkcja 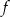ma następujące własności:
1. Dziedziną funkcji jest przedział 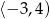⟨− 3,4) .
2. Przedział 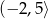(− 2,5⟩ jest zbiorem wartości funkcji .
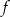3. Funkcja ma dwa miejsca zerowe -2 oraz 3.
4. Funkcja 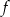jest rosnąca w przedziale 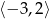⟨− 3,2⟩ i malejąca w przedziale 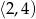⟨2,4) . Podaj zbiór rozwiązań nierówności f (x) > 0 .

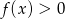Zadanie 4

(5 pkt)

Wyznaczyć dziedzinę funkcji 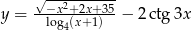√-−x2+2x+35- y = log4(x+1) − 2 ctg 3x .

Zadanie 5

(6 pkt)

Wyznacz dziedzinę funkcji

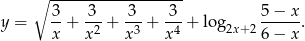
∘ ------------------- y = 3-+ 3--+ -3-+ 3-+ lo g 5−--x. x x2 x3 x4 2x+2 6− x

Zadanie 6

(3 pkt)

Z równania 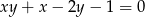xy+ x − 2y − 1 = 0 wyznacz 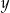jako funkcję zmiennej . Wyznacz jej dziedzinę oraz współrzędne punktów przecięcia wykresu z osiami układu współrzędnych.

Rozwiąż on-line Arkusz Wersja PDF