Zestaw użytkownika nr 1442_9786
Wielomiany - sprawdzian (podstawa, zadania zamknięte)
Pierwiastkami wielomianu stopnia trzeciego 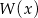 są liczby 2,-1,-3, a współczynnik stojący przy najwyższej potędze zmiennej
są liczby 2,-1,-3, a współczynnik stojący przy najwyższej potędze zmiennej  jest równy 4. Wielomian ten można zapisać w postaci
jest równy 4. Wielomian ten można zapisać w postaci
A) 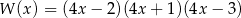
B) 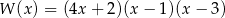
C) 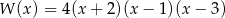
D) 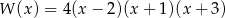
Dane są wielomiany 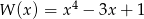 oraz
oraz 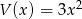 . Wielomian
. Wielomian 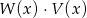 jest równy
jest równy
A) 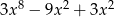 B)
B) 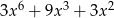 C)
C) 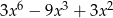 D)
D) 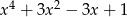
Stopień wielomianu 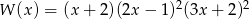 jest równy
jest równy
A) 8 B) 4 C) 6 D) 5
Wielomiany 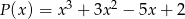 i
i 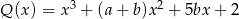 są równe. Zatem
są równe. Zatem
A) 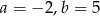 B)
B) 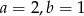 C)
C) 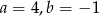 D)
D) 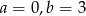
Wielomian 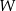 określony jest wzorem
określony jest wzorem 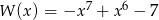 . Zatem
. Zatem 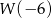 jest liczbą
jest liczbą
A) ujemną B) dodatnią C) pierwszą D) niewymierną
Funkcja 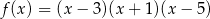
A) ma 3 miejsca zerowe
B) nie ma miejsc zerowych
C) ma 2 miejsca zerowe
D) ma 1 miejsce zerowe
Który z wielomianów należy dodać do wielomianu 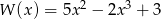 aby otrzymać wielomian
aby otrzymać wielomian 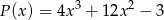 ?
?
A) 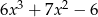 B)
B) 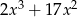 C)
C) 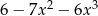 D)
D) 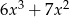
Wiadomo, że 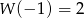 , gdy
, gdy 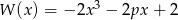 . Zatem wartość współczynnika
. Zatem wartość współczynnika 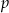 wynosi:
wynosi:
A) -1 B) 3 C) -3 D) 6
Ile pierwiastków ma wielomian 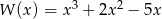 ?
?
A) 2 B) 0 C) 3 D) 1
Suma pierwiastków wielomianu 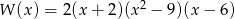 jest równa
jest równa
A) 4 B) 5 C) 8 D) -4
Pierwiastkami równania 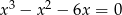 są liczby
są liczby
A) 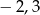 B)
B) 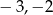 C)
C) 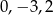 D)
D) 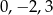
Równanie 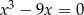
A) nie ma pierwiastków
B) ma jeden pierwiastek
C) ma dwa pierwiastki
D) ma trzy pierwiastki
Rozwiąż nierówność 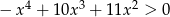 .
.
Rozwiąż równanie 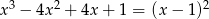 .
.

