Zestaw użytkownika nr 1555_1965

Zestaw użytkownika
nr 1555_1965

Zadanie 1

Obwód czworokąta wypukłego 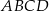ABCD jest równy 50 cm. Obwód trójkąta 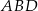ABD jest równy 46 cm, a obwód trójkąta 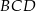BCD jest równy 36 cm. Oblicz długość przekątnej .

Zadanie 2

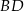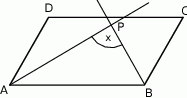
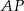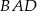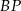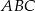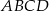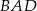Półprosta jest dwusieczną kąta BAD i półprosta jest dwusieczną kąta ABC w równoległoboku ABCD . Kąt BAD jest równy 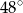48∘ . Oblicz miarę kąta 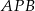AP B . Zapisz obliczenia.

Zadanie 3

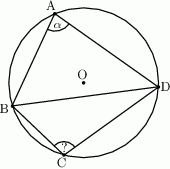
Wszystkie wierzchołki czworokąta 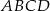ABCD leżą na okręgu oraz 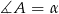∡A = α . Oblicz miarę kąta .

Zadanie 4

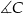Obwód trapezu równoramiennego wynosi 32 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 3 cm i 11 cm. Oblicz pole trapezu.

Zadanie 5

Różnica między polem koła opisanego na kwadracie a polem koła wpisanego w kwadrat jest równa 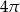. Oblicz pole kwadratu.

Zadanie 6

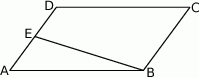
Punkt 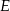jest środkiem boku 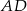równoległoboku 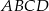ABCD . Pole trójkąta 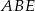ABE jest równe 2. Oblicz pole równoległoboku.

Zadanie 7

Obwód rombu wynosi 18 cm, a jego pole 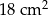2 18 cm . Oblicz wysokość tego rombu.

Zadanie 8

W trójkącie równoramiennym wysokość poprowadzona do podstawy ma długość 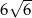√ -- 6 6 . Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.

Zadanie 9

Oblicz pole trójkąta równoramiennego, w którym odległość wierzchołka kąta prostego od przeciwprostokątnej jest równa 5 cm.

Zadanie 10

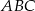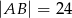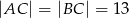Oblicz pole trójkąta równoramiennego ABC , w którym |AB | = 24 i |AC | = |BC | = 13 .

Zadanie 11

Prosta 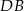jest styczna do okręgu w punkcie 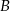. Oblicz miarę zaznaczonego kąta 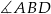∡ABD jeśli ∡ACB = α .

Zadanie 12

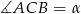Dane są dwa okręgi zewnętrznie styczne oraz styczne wewnętrznie do trzeciego. Środki okręgów tworzą trójkąt równoramienny o bokach długości 1 i 2. Znajdź długości promieni tych okręgów (rozważ dwa przypadki).

Zadanie 13

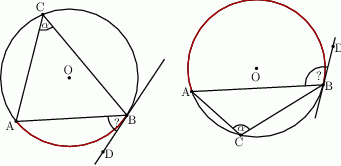
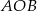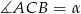Oblicz miary kątów środkowych AOB zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego ∡ACB = α .

Arkusz Wersja PDF