Zestaw użytkownika nr 1561_9155
Sprawdzian-prawdopodobieństwo6 Grudnia 2011Czas pracy: 45 min.Suma punktów: 19
Wybieramy liczbę  ze zbioru
ze zbioru 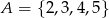 oraz liczbę
oraz liczbę 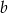 ze zbioru
ze zbioru 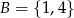 . Ile jest takich par
. Ile jest takich par 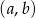 , że iloczyn
, że iloczyn 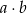 jest liczbą nieparzystą?
jest liczbą nieparzystą?
A) 2 B) 3 C) 20 D) 5
Ze zbioru liczb 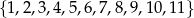 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 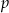 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 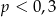 B)
B) 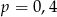 C)
C) 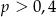 D)
D) 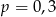
Z talii 52 kart losujemy jedną. Prawdopodobieństwo tego, że wylosujemy kartę trefl lub waleta lub króla, jest równe
A) 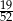 B)
B) 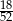 C)
C) 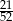 D)
D) 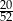
O zdarzeniach losowych 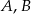 wiadomo, że:
wiadomo, że: 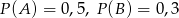 i
i 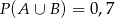 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 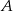 i
i 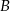 spełnia warunek
spełnia warunek
A) 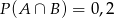 B)
B) 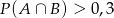 C)
C) 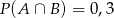 D)
D) 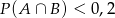
W pewnej szkole 20% uczniów klas trzecich pisało maturę próbną z matematyki, przy czym 90% spośród piszących otrzymało z próbnej matury więcej niż 35 punktów. Spośród wszystkich uczniów klas trzecich wybrano losowo jednego ucznia. Prawdopodobieństwo, że wybrano ucznia, który pisał maturę próbną z matematyki i otrzymał więcej niż 35 punktów jest równe
A) 0,18 B) 0,9 C) 0,45 D) 0,72
W pewnej grupie uczniów każdy zna język angielski lub niemiecki. Wiadomo, że prawdopodobieństwo wylosowania z tej grupy ucznia znającego język angielski jest równe  , natomiast prawdopodobieństwo wylosowania ucznia znającego język niemiecki jest równe
, natomiast prawdopodobieństwo wylosowania ucznia znającego język niemiecki jest równe  . Jakie jest prawdopodobieństwo tego, że losowo wybrany uczeń zna obydwa języki?
. Jakie jest prawdopodobieństwo tego, że losowo wybrany uczeń zna obydwa języki?
Rzucamy dwukrotnie sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma liczb oczek otrzymanych na obu kostkach jest większa od 6 i iloczyn tych liczb jest nieparzysty.
W dwóch urnach znajdują się kule białe i czarne, przy czym w pierwszej jest 6 kul białych i 4 czarne, a w drugiej urnie 5 białych i 5 czarnych. Rzucamy raz symetryczną kostką do gry. Jeżeli wyrzucimy co najmniej 4 oczka to losujemy 2 kule z pierwszej urny, a jeżeli wyrzucimy co najwyżej 3 oczka to losujemy 2 kule z drugiej urny. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.
Do kina wybrało się 7 osób, wśród nich Basia i Janek. Wszyscy usiedli w jednym rzędzie, w którym jest dokładnie 7 wolnych miejsc. Oblicz, na ile sposobów wymienione osoby mogą zająć miejsca tak, by Basia i Janek siedzieli obok siebie. Oblicz też prawdopodobieństwo tego, że przy losowym zajmowaniu miejsc Basia i Janek nie siedzą obok siebie.

