Zestaw użytkownika nr 1573_7353

Liczby powtórzenie Suma punktów: 55

Zadanie 1
(5 pkt)

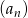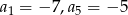Znajdź ogólny wyraz ciągu arytmetycznego (an) wiedząc, że a1 = −7 ,a5 = − 5 .

Zadanie 2
(5 pkt)

Piąty wyraz ciągu arytmetycznego jest równy 26, a suma pięciu początkowych wyrazów tego ciągu jest równa 70. Oblicz pierwszy wyraz tego ciągu.

Zadanie 3
(5 pkt)

Wyrazami ciągu arytmetycznego 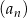(an) są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 2. Ponadto 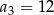a3 = 12 . Oblicz a15 .

Zadanie 4
(5 pkt)

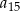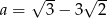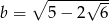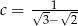Wykaż, że liczby √ -- √ -- a = 3 − 3 2 , ∘ -----√--- b = 5 − 2 6 i ---1--- c = √3− √2 są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.

Zadanie 5
(5 pkt)

Drugi wyraz ciągu arytmetycznego jest równy -3, dziesiąty wyraz jest równy 21. Wyznacz pierwszy wyraz i różnicę tego ciągu.

Zadanie 6
(5 pkt)

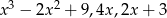Liczby 3 2 x − 2x + 9,4x,2x + 3 są kolejnymi wyrazami malejącego ciągu arytmetycznego. Oblicz x .

Zadanie 7
(5 pkt)

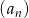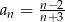Ciąg (an) określony jest wzorem n−-2 an = n+ 3 .

  1. Oblicz dziesiąty wyraz ciągu.
  2. Oblicz, który wyraz ciągu jest równy 4 9 .
Zadanie 8
(5 pkt)

Pierwszy wyraz niemonotonicznego ciągu geometrycznego 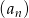(an) jest równy 48 i jest o 36 większy od wyrazu trzeciego.

  • Oblicz iloraz ciągu (an ) .
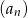  • Oblicz ósmy wyraz ciągu (a ) n .
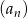  • Suma kilku początkowych wyrazów ciągu 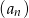(an) jest równa 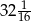1- 3 216 . Oblicz, ile wyrazów zsumowano.
Zadanie 9
(5 pkt)

Wykaż, że liczby 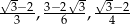√-3−2 3−-2√3 √-3−2 3 , 6 , 4 są kolejnymi wyrazami ciągu geometrycznego.

Zadanie 10
(5 pkt)

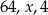Liczby 64,x,4 są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.

Zadanie 11
(5 pkt)

Oblicz

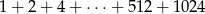  • 1+ 2+ 4+ ⋅⋅⋅+ 5 12+ 1024 ,
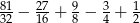  • 81− 27+ 9 − 3 + 1 32 16 8 4 2 .
Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze