Zestaw użytkownika nr 1641_3798
Zestaw użytkownika
nr 1641_3798
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.
Podstawą graniastosłupa jest trójkąt prostokątny równoramienny o ramieniu długości 9. Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 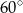 . Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
. Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.
W kulę o promieniu długości 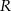 wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
Podstawą ostrosłupa 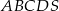 jest kwadrat
jest kwadrat 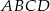 (patrz rysunek).
(patrz rysunek).
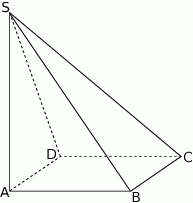
Krawędź 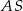 jest wysokością tego ostrosłupa. Odległość punktu
jest wysokością tego ostrosłupa. Odległość punktu 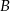 od krawędzi
od krawędzi 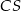 jest równa
jest równa 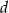 , a kąt dwuścienny między ścianami
, a kąt dwuścienny między ścianami 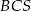 i
i 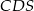 ma miarę
ma miarę 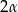 , gdzie
, gdzie 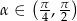 . Oblicz:
. Oblicz:
- odległość punktu
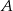 od krawędzi
od krawędzi 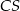
- wysokość tego ostrosłupa.
Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości  . Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Jakie powinny być długości pozostałych krawędzi graniastosłupa, aby jego objętość była największa?
. Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Jakie powinny być długości pozostałych krawędzi graniastosłupa, aby jego objętość była największa?
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest półkolem. Oblicz miarę kąta rozwarcia stożka.
W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość 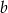 , a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę
, a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Liczba wszystkich przekątnych podstaw i ścian bocznych pewnego graniastosłupa jest równa 110. Oblicz, ile krawędzi ma podstawa tego graniastosłupa.
Oblicz objętość ostrosłupa prawidłowego czworokątnego jeśli jego krawędź boczna o długości 6 nachylona jest do płaszczyzny podstawy pod kątem 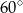 .
.
Przekrój stożka wyznaczony przez wierzchołek i cięciwę podstawy jest trójkątem równobocznym, o polu równym 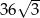 . Płaszczyzna
. Płaszczyzna  , do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej
, do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej 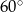 . Oblicz objętość stożka.
. Oblicz objętość stożka.
W kulę o promieniu 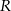 wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem
wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem  . Oblicz objętość stożka.
. Oblicz objętość stożka.
Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 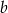 i tworzy z krawędzią podstawy kąt o mierze
i tworzy z krawędzią podstawy kąt o mierze  . Jaką objętość ma ten ostrosłup?
. Jaką objętość ma ten ostrosłup?
W sferę o promieniu 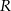 wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość
wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość 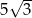 , oblicz
, oblicz 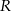 .
.

