Zestaw użytkownika nr 1674_6807
Zestaw użytkownika
nr 1674_6807
Z talii pięćdziesięciu dwu kart wyciągnięto losowo trzy karty. Oblicz prawdopodobieństwo wyciągnięcia dokładnie jednego króla.
Z talii 52 kart wyciągamy losowo jedną. Oblicz prawdopodobieństwo, że wyciągnięta karta będzie damą lub treflem.
Losujemy jedną z 52 kart. Jakie jest prawdopodobieństwo wyciągnięcia asa lub króla?
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia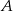
– na każdej kostce wypadła nieparzysta liczba oczek,
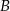– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia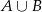 
.
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 12.
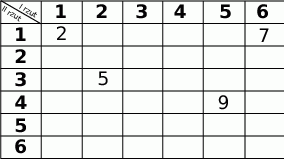
Rzucamy dwa razy symetryczną, sześcienną kostką do gry i zapisujemy sumę liczb wyrzuconych oczek.
- Uzupełnij tabelę, tak aby przedstawiała wszystkie możliwe wyniki tego doświadczenia.
- Oblicz prawdopodobieństwo zdarzenia
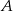, polegającego na tym, że suma liczb oczek jest liczbą nieparzystą. - Oblicz prawdopodobieństwo zdarzenia
, polegającego na tym, że reszta z dzielenia sumy liczby oczek przez 3 jest równa 2.
Oblicz prawdopodobieństwo, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 4.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo każdego z następujących zdarzeń:
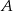— w każdym rzucie wypadnie nieparzysta liczba oczek. 
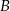-– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9. 
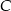-– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.
Rzucamy dwukrotnie kostką, które ze zdarzeń jest bardziej prawdopodobne: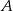
– w pierwszym rzucie otrzymamy liczbę oczek mniejszą niż w drugim;
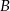– suma oczek, jakie wypadną w obydwu rzutach, jest nie mniejsza od 8?
Na loterii jest 40 losów, w tym 4 wygrywające. Kupujemy 2 losy. Jakie jest prawdopodobieństwo tego, że będzie wśród nich dokładnie jeden los wygrywający?
Spośród 5 monet jednozłotowych, 7 dwuzłotowych i 6 pięciozłotowych wybieramy 3 monety. Oblicz prawdopodobieństwo, że wszystkie trzy monety będą miały ten sam nominał.
Co jest bardziej prawdopodobne: wyrzucić dwa orły w trzech rzutach monetą, czy trzy orły w czterech rzutach?
Rzucono 8 razy monetą. Oblicz prawdopodobieństwo tego, że co najmniej jeden raz wyrzucono orła.
Z urny, w której jest 6 kul czarnych i 4 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule jednakowych kolorów.
W urnie znajduję się 5 kul białych i 3 czarne. Wyjmujemy losowo 4 kule. Oblicz prawdopodobieństwo, że wśród wyjętych są przynajmniej 2 kule czarne.
W jednej urnie są 3 kule: czerwona, biała i zielona, a w drugiej urnie są 2 kule: czerwona i biała. Losujemy po jednej kuli z każdej urny. Jakie jest prawdopodobieństwo wyciągnięcia dwóch kul w tym samym kolorze?
W urnie znajduje się 5 kul białych, 3 kule czerwone i 1 zielona. Losujemy 1 kulę. Oblicz prawdopodobieństwo wylosowania kuli białej.
