Zestaw użytkownika nr 1728_7206
Zestaw użytkownika
nr 1728_7206
Dany jest odcinek o końcach 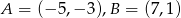 .
.
- Wyznacz równanie symetralnej tego odcinka.
- Wyznacz równanie okręgu o średnicy
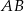 .
.
Wyznacz równanie symetralnej odcinka o końcach 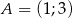 i
i 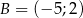 .
.
Dane są punkty 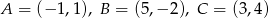 .
.
- Wyznacz równanie prostej przechodzącej przez punkt
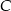 i prostopadłej do prostej
i prostopadłej do prostej 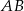 .
. - Oblicz pole trójkąta
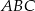 .
.
W równoległoboku 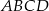 dane są wierzchołki
dane są wierzchołki 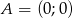 ,
, 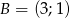 ,
, 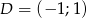 . Wyznacz wierzchołek
. Wyznacz wierzchołek 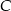 oraz środek symetrii tego równoległoboku.
oraz środek symetrii tego równoległoboku.
Środek 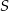 okręgu
okręgu 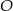 należy do prostej
należy do prostej 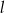 o równaniu
o równaniu 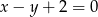 . Punkty
. Punkty 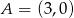 i
i 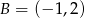 należą do tego okręgu.
należą do tego okręgu.
- Wyznacz równanie okręgu
 .
. - Wyznacz współrzędne takiego punktu
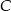 należącego do okręgu
należącego do okręgu 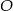 , że
, że 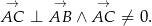
- Wyznacz równania stycznych
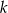 i
i 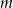 do okręgu
do okręgu 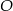 takich, że
takich, że 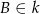 i
i 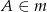 oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
Dla jakich wartości parametru 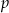 proste
proste 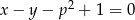 i
i 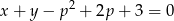 przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach
przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach 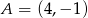 ,
, 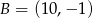 ,
, 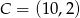 ,
, 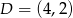 ?
?
Określ wzajemne położenie prostej 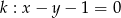 i okręgu o równaniu
i okręgu o równaniu 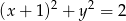 .
.
Zapisz równanie prostej przechodzącej przez punkt 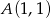 i równoległej do prostej danej równaniem
i równoległej do prostej danej równaniem 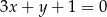 .
.
Wiadomo, że okrąg jest styczny do prostej o równaniu 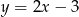 w punkcie
w punkcie 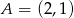 i styczny do prostej o równaniu
i styczny do prostej o równaniu 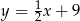 w punkcie
w punkcie 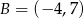 . Oblicz promień tego okręgu.
. Oblicz promień tego okręgu.
Wykaż, że trójkąt 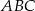 o wierzchołkach
o wierzchołkach 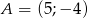 ,
, 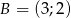 ,
, 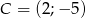 jest prostokątny.
jest prostokątny.
Wyznacz równanie okręgu o środku 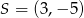 przechodzącego przez początek układu współrzędnych.
przechodzącego przez początek układu współrzędnych.

