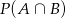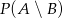Zestaw użytkownika nr 1752_2242
Zestaw użytkownika
nr 1752_2242
Oblicz, ile jest liczb naturalnych pięciocyfrowych, w zapisie których nie występuje zero, jest dokładnie jedna cyfra 7 i dokładnie jedna cyfra parzysta.
Na ile sposobów można umieścić w 7 szufladach 3 bluzki tak, aby każda była w innej szufladzie?
Pan Eugeniusz szykując się rano do pracy wybiera jeden spośród swoich 12 zegarków oraz dwa spośród 22 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 34 B) 2777 C) 5544 D) 5808
Na ile sposobów można ustawić na półce 5 tomów encyklopedii tak, aby tomy 3 i 4 stały obok siebie (w dowolnej kolejności)?
A) 120 B) 60 C) 48 D) 24
Na regale można ustawić  książek na 24 sposoby. Zatem
książek na 24 sposoby. Zatem
A) 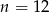 B)
B) 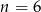 C)
C) 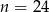 D)
D) 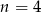
Dane są zbiory liczb całkowitych: 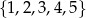 i
i 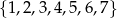 . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
. Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
W koszu znajdują się owoce: 12 jabłek i 8 pomarańczy. Wyjmujemy kolejno trzy owoce, nie odkładając ich do kosza. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwie pomarańcze.
O zdarzeniach losowych 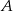 i
i 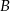 wiemy, że:
wiemy, że: 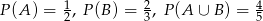 . Oblicz:
. Oblicz:
W garderobie pani Joanny wiszą 3 żakiety: biały, zielony i granatowy oraz 4 spódnice: czarna, biała, granatowa i szara. Oblicz prawdopodobieństwo zdarzenia, że wybierając losowo jeden żakiet i jedną spódnicę, pani Joanna skompletuje strój w jednym kolorze.
10 kul rozmieszczamy w 10 szufladach. Jakie jest prawdopodobieństwo tego, że każda szuflada będzie zajęta?
Wiadomo, że 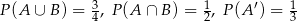 . Oblicz prawdopodobieństwa zdarzeń
. Oblicz prawdopodobieństwa zdarzeń 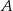 i
i 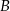 .
.
W pewnej grupie uczniów każdy zna język angielski lub niemiecki. Wiadomo, że prawdopodobieństwo wylosowania z tej grupy ucznia znającego język angielski jest równe  , natomiast prawdopodobieństwo wylosowania ucznia znającego język niemiecki jest równe
, natomiast prawdopodobieństwo wylosowania ucznia znającego język niemiecki jest równe  . Jakie jest prawdopodobieństwo tego, że losowo wybrany uczeń zna obydwa języki?
. Jakie jest prawdopodobieństwo tego, że losowo wybrany uczeń zna obydwa języki?
Z cyfr 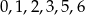 tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
Wiedząc, że 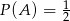 ,
, 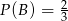 ,
, 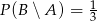 , oblicz
, oblicz 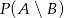 .
.
Rzucamy 7 razy dwiema monetami. Oblicz prawdopodobieństwo, że co najmniej 6 razy wyrzucimy dwie reszki.
Windą, zatrzymującą się na 6 piętrach, jadą 4 osoby. Jakie jest prawdopodobieństwo tego, że każda osoba wysiądzie na innym piętrze?
Piotrek ma 100 płyt CD z muzyką poważną. Codziennie słucha jednej płyty i odstawia ją na miejsce. Płyty wybiera w sposób losowy. Oblicz prawdopodobieństwo, że w ciągu pięciu kolejnych dni będzie słuchał codziennie tej samej płyty.
Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 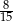 , a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe 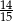 . Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej jest równe
A) 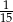 B)
B) 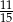 C)
C) 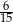 D)
D) 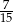
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 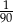 B)
B) 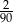 C)
C) 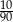 D)
D) 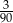
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równej trzy wynosi
A) 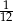 B)
B)  C)
C) 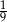 D)
D)