Zestaw użytkownika nr 1820_4230
Geometria analityczna - powtórzenie
W układzie współrzędnych dane są dwa punkty: 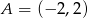 i
i 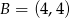 .
.
- Wyznacz równanie symetralnej odcinka
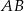 .
. - Prosta
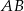 oraz prosta o równaniu
oraz prosta o równaniu 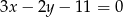 przecinają się w punkcie
przecinają się w punkcie  . Oblicz współrzędne punktu
. Oblicz współrzędne punktu  .
.
Wyznacz równanie prostej równoległej do prostej 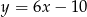 przechodzącej przez punkt
przechodzącej przez punkt 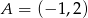 oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt
oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt 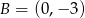 .
.
Zapisz równanie prostej przechodzącej przez punkt 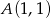 i równoległej do prostej danej równaniem
i równoległej do prostej danej równaniem 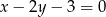 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 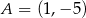 oraz
oraz 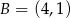 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 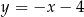 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Punkty 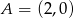 i
i 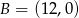 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 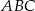 o przeciwprostokątnej
o przeciwprostokątnej 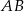 . Wierzchołek
. Wierzchołek 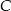 leży na prostej o równaniu
leży na prostej o równaniu 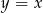 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu  .
.
Oblicz pole i obwód trójkąta o wierzchołkach: 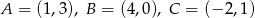 .
.
Napisz równanie wysokości trójkąta o wierzchołkach 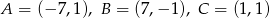 opuszczonej z wierzchołka
opuszczonej z wierzchołka 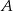 .
.
Oblicz pole trójkąta o wierzchołkach 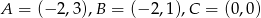 .
.
Dane są dwa przeciwległe wierzchołki kwadratu 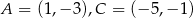 . Wyznacz obwód tego kwadratu.
. Wyznacz obwód tego kwadratu.
Współrzędne przeciwległych wierzchołków prostokąta 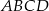 są równe
są równe 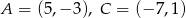 . Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek
. Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek 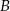 leży na prostej
leży na prostej 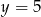 .
.
W kwadracie 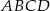 dane są wierzchołek
dane są wierzchołek 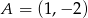 i środek symetrii
i środek symetrii 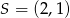 . Oblicz pole kwadratu
. Oblicz pole kwadratu 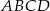 .
.
Wyznacz równanie okręgu opisanego na prostokącie 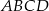 , w którym
, w którym 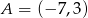 i
i 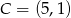 .
.
Napisz równanie okręgu o promieniu 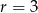 , stycznego do obu osi układu.
, stycznego do obu osi układu.
Znajdź równanie okręgu o środku w punkcie 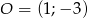 , wiedząc, że okrąg jest styczny do prostej
, wiedząc, że okrąg jest styczny do prostej 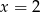 .
.
Wyznacz równanie okręgu stycznego do osi 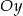 , którego środkiem jest punkt
, którego środkiem jest punkt 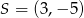 .
.
Punkty 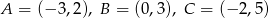 to wierzchołki trójkąta. Podaj, jakie są współrzędne wierzchołków trójkąta symetrycznego do trójkąta
to wierzchołki trójkąta. Podaj, jakie są współrzędne wierzchołków trójkąta symetrycznego do trójkąta 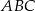 względem
względem
- osi
 ,
, - osi
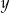 ,
, - punktu
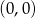 .
.
Wyznacz równanie okręgu symetrycznego do okręgu 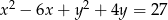 względem prostej
względem prostej 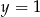 .
.

