Zestaw użytkownika nr 1866_2589
LiczbyLiczby naturalne12 Listopada 2011Czas pracy: 180 min.
Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 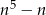 jest podzielna przez 5.
jest podzielna przez 5.
Wykaż, że iloczyn trzech kolejnych liczb podzielnych przez 3 dzieli się przez 81.
Uzasadnij, że dla dowolnych liczb naturalnych 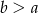 zachodzi równość
zachodzi równość 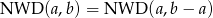 .
.
Wykaż, że jeżeli liczby całkowite 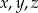 spełniają równanie
spełniają równanie 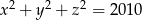 to co najwyżej jedna z liczb
to co najwyżej jedna z liczb 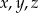 dzieli się przez 4.
dzieli się przez 4.
Wykaż, że różnica kwadratów dwóch kolejnych liczb parzystych jest liczbą podzielną przez 4.
Wykaż, że różnica kwadratów dwóch kolejnych liczb nieparzystych jest liczbą podzielną przez 8.
Wykaż, że liczba 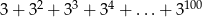 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że suma kwadratów dwóch kolejnych liczb nieparzystych nie dzieli się przez 4.
Pokazać, że dla każdej liczby naturalnej  liczba
liczba 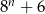 jest podzielna przez 7.
jest podzielna przez 7.
Wykaż, że każda liczba pierwsza większa od 3 jest postaci 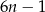 lub
lub 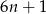 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej  .
.
Wykaż, że jeśli  należy do zbioru liczb całkowitych, to
należy do zbioru liczb całkowitych, to 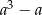 jest podzielne przez 3.
jest podzielne przez 3.
Wykaż, że liczba 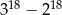 jest podzielna przez 19.
jest podzielna przez 19.
Wyznacz wszystkie liczby całkowite  , dla których liczba
, dla których liczba 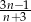 jest liczbą całkowitą.
jest liczbą całkowitą.
Liczby naturalne dodatnie 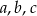 spełniają równanie
spełniają równanie 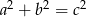 . Uzasadnij, że liczba
. Uzasadnij, że liczba 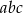 jest
jest
- parzysta;
- podzielna przez 3.
Wykaż, że suma pięciu kolejnych liczb naturalnych nie może być liczbą pierwszą.
Uzasadnij, że liczba 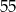 jest dzielnikiem liczby 31!, i że liczba 37 nie jest dzielnikiem liczby 31!.
jest dzielnikiem liczby 31!, i że liczba 37 nie jest dzielnikiem liczby 31!.
Wykaż, że liczba 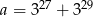 jest podzielna przez 30.
jest podzielna przez 30.
Wykaż, że liczba 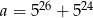 jest podzielna przez 130.
jest podzielna przez 130.
Niech 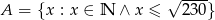 i
i 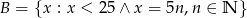 . Wyznacz zbiory
. Wyznacz zbiory 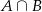 oraz
oraz 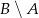 .
.
Wykaż, że 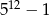 jest liczbą podzielną przez 31.
jest liczbą podzielną przez 31.
Wykaż, że jeżeli  jest liczbą nieparzystą to liczba
jest liczbą nieparzystą to liczba
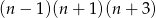
jest liczbą podzielną przez 48.
Wykaż, że liczba 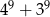 jest podzielna przez 91.
jest podzielna przez 91.
Wykaż, że liczba 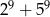 jest podzielna przez 133.
jest podzielna przez 133.
Wykaż, że dla dowolnej liczby całkowitej 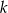 różnica iloczynu tej liczby i liczby od niej o 3 większej oraz iloczynu dwóch kolejnych liczb całkowitych większych od
różnica iloczynu tej liczby i liczby od niej o 3 większej oraz iloczynu dwóch kolejnych liczb całkowitych większych od 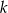 jest równa -2.
jest równa -2.
Uzasadnij, że dla każdej liczby całkowitej 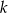 liczba
liczba 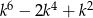 jest podzielna przez 36.
jest podzielna przez 36.
Wykaż, że jeżeli 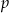 jest liczbą pierwszą większą od 3 to
jest liczbą pierwszą większą od 3 to 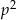 przy dzieleniu przez 24 daje resztę 1.
przy dzieleniu przez 24 daje resztę 1.
Wykaż, że liczba 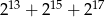 jest podzielna przez 21.
jest podzielna przez 21.
Wykaż, że kwadrat liczby całkowitej dającej z dzielenia przez 3 resztę 2, przy dzieleniu przez 3 daje resztę 1.
Uzasadnij, że jeżeli  jest liczbą naturalną to liczba
jest liczbą naturalną to liczba 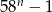 dzieli się przez 19.
dzieli się przez 19.
Wykaż, że jeżeli przy dzieleniu przez 7 jedna liczba daję resztę 3, a druga resztę 4, to iloczyn tych liczb daje przy dzieleniu przez 7 resztę 5.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 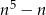 jest podzielna przez 30.
jest podzielna przez 30.
Wykaż, że reszta z dzielenia sumy kwadratów trzech kolejnych liczb naturalnych przez 3 jest równa 2.
Uzasadnij, że suma kwadratów dwóch kolejnych nieparzystych liczb całkowitych nie może być kwadratem liczby całkowitej.
Udowodnij, że jeśli 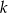 i
i  są liczbami naturalnymi oraz
są liczbami naturalnymi oraz 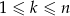 , to
, to 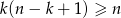 .
.
Udowodnij, że dla każdej liczby naturalnej  , liczba
, liczba 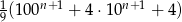 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Uzasadnij, że jeżeli  jest liczbą całkowitą to liczba
jest liczbą całkowitą to liczba 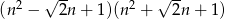 też jest liczbą całkowitą.
też jest liczbą całkowitą.

