Zestaw użytkownika nr 1875_4204
Zestaw użytkownika
nr 1875_4204
Zadanie 1
Napisz wzór funkcji liniowej o współczynniku kierunkowym 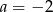 , której wykres przecina oś
, której wykres przecina oś 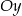 w punkcie
w punkcie 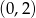 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
Zadanie 2
Rozstrzygnij czy wykresy funkcji 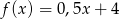 ,
, 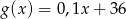 i
i 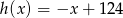 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Zadanie 3
O funkcji liniowej 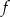 wiadomo, że
wiadomo, że 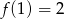 oraz, że do wykresu tej funkcji należy punkt
oraz, że do wykresu tej funkcji należy punkt 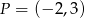 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 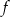 .
.
Zadanie 4
Napisz wzór funkcji liniowej, której wykres przechodzi przez punkty 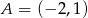 i
i 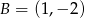 .
.
Zadanie 5
Wyznacz wzór funkcji liniowej o współczynniku kierunkowym 2 i przechodzącej przez punkt 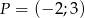 .
.
Zadanie 6
Wykres funkcji liniowej 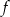 przecina osie
przecina osie 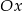 i
i 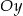 układu współrzędnych odpowiednio w punktach
układu współrzędnych odpowiednio w punktach 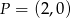 oraz
oraz 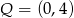 .
.
- Wyznacz wzór funkcji
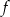 .
. - Sprawdź, czy dla argumentu
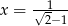 wartość funkcji
wartość funkcji 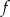 wynosi
wynosi 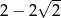 .
.

