Zestaw użytkownika nr 1895_3389
Wyrażenia algebraiczne
Liczby 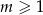 i
i 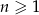 spełniają warunek
spełniają warunek 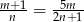 . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 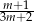 B)
B) 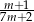 C)
C) 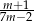 D)
D) 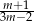
Wyrażenie 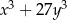 jest równe iloczynowi
jest równe iloczynowi
A) 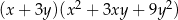
B) 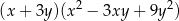
C) 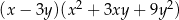
D) 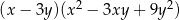
Wyrażenie 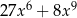 można zapisać w postaci
można zapisać w postaci
A) 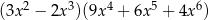
B) 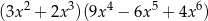
C) 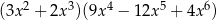
D) 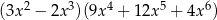
Wiadomo, że 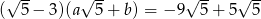 oraz
oraz  i
i 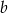 są liczbami wymiernymi. Zatem
są liczbami wymiernymi. Zatem
A) 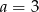 i
i 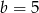 B)
B) 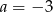 i
i 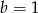 C)
C) 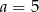 i
i 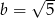 D)
D) 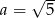 i
i 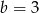
Wyrażenie 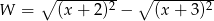 dla
dla 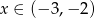 przyjmuje postać
przyjmuje postać
A) 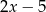 B)
B) 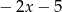 C)
C) 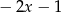 D) -1
D) -1
Wyrażenie wymierne 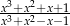 po uproszczeniu ma postać:
po uproszczeniu ma postać:
A) 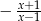 B)
B) 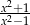 C)
C) 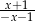 D)
D) 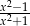
Po wykonaniu działań w wyrażeniu 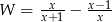 otrzymujemy
otrzymujemy
A) 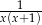 B)
B) 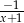 C)
C) 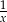 D)
D) 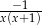
Wartość wyrażenia 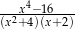 dla
dla 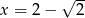 jest równa
jest równa
A) 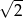 B) 2 C) -2 D)
B) 2 C) -2 D) 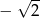
Po skróceniu wyrażenia 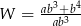 otrzymamy
otrzymamy
A) 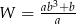 B)
B) 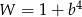 C)
C) 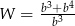 D)
D) 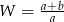
Wiadomo, że 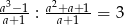 . Zatem
. Zatem 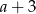 jest równe
jest równe
A) 7 B) 1 C) 5 D) -1
Wyrażenie 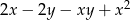 jest równe wyrażeniu
jest równe wyrażeniu
A) 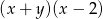 B)
B) 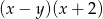 C)
C) 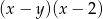 D)
D) 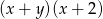
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 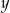 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 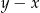 B)
B) 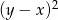 C)
C) 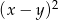 D)
D) 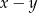
Sześcian wyrażenia 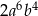 jest równy
jest równy
A) 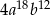 B)
B) 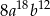 C)
C) 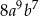 D)
D) 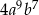
Połowę liczby  zwiększono o 20%. Otrzymano
zwiększono o 20%. Otrzymano
A) 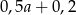 B)
B) 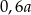 C)
C) 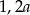 D)
D) 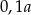
Jeżeli liczba 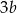 jest o 20% większa od połowy liczby
jest o 20% większa od połowy liczby 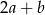 , to liczba
, to liczba  jest większa od
jest większa od 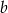 o
o
A) 80% B) 50% C) 100% D) 200%
Jeżeli 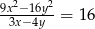 , to
, to
A) 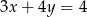 B)
B) 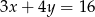 C)
C) 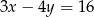 D)
D) 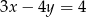
Wyrażenie 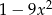 po rozłożeniu na czynniki liniowe ma postać:
po rozłożeniu na czynniki liniowe ma postać:
A) 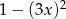 B)
B) 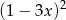 C)
C) 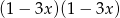 D)
D) 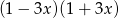
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 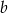 . O ile procent liczba
. O ile procent liczba 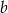 jest większa od liczby
jest większa od liczby  ?
?
A) 20% B) 120% C) 25% D) 80%
Wiadomo, że 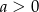 . Wyrażenie
. Wyrażenie 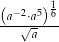 po sprowadzeniu do najprostszej postaci jest równe
po sprowadzeniu do najprostszej postaci jest równe
A)  B)
B) 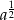 C) 0 D) 1
C) 0 D) 1
Wyrażenie 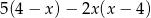 można zapisać w postaci
można zapisać w postaci
A) 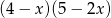 B)
B) 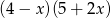 C)
C) 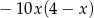 D)
D) 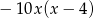
Liczba  przy dzieleniu przez 5 daje resztę 3. Liczbę
przy dzieleniu przez 5 daje resztę 3. Liczbę  można więc zapisać w postaci
można więc zapisać w postaci 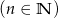
A) 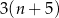 B)
B) 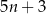 C)
C) 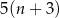 D)
D) 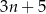
Wyrażenie 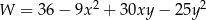 w postaci iloczynowej ma postać
w postaci iloczynowej ma postać
A) 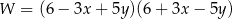
B) 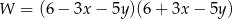
C) 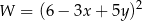
D) 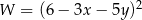
Zdanie: „Liczba  jest o 8 większa od potrojonego kwadratu liczby
jest o 8 większa od potrojonego kwadratu liczby  ” zapisane w postaci równania to
” zapisane w postaci równania to
A) 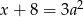 B)
B) 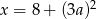 C)
C) 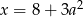 D)
D) 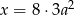
Suma wyrażeń 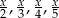 jest równa
jest równa
A) 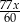 B)
B) 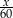 C)
C) 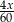 D)
D) 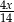
Wyrażenie 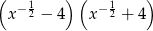 , dla
, dla 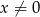 , można zapisać w postaci
, można zapisać w postaci
A) 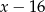 B)
B) 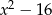 C)
C) 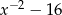 D)
D) 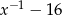
Liczbę naturalną  najpierw zwiększono o 40%, a następnie zmniejszono o 20%. W wyniku tych operacji liczbę
najpierw zwiększono o 40%, a następnie zmniejszono o 20%. W wyniku tych operacji liczbę 
A) zmniejszono o 12%
B) zmniejszono o 30%
C) zwiększono o 12%
D) zwiększono o 20%
Liczba 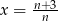 jest liczbą naturalną. Liczb naturalnych
jest liczbą naturalną. Liczb naturalnych  spełniających warunki zadania
spełniających warunki zadania
A) są trzy B) nie ma C) są dwie D) jest nieskończenie wiele
Wyrażenie 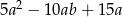 jest równe iloczynowi
jest równe iloczynowi
A) 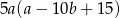 B)
B) 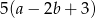 C)
C) 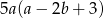 D)
D) 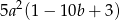
Wartością wyrażenia 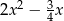 dla
dla 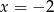 jest liczba:
jest liczba:
A) 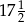 B)
B) 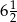 C)
C) 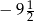 D)
D) 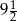
Wyrażenie 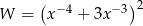 jest równe
jest równe
A) 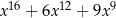
B) 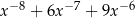
C) 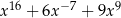
D) 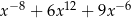
Uzasadnij, że dla każdej liczby 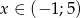 wyrażenie
wyrażenie 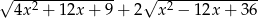 ma stałą wartość.
ma stałą wartość.
Skróć ułamek 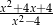 .
.
Skróć ułamek: 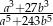 .
.
Zapisz wyrażenie w prostszej postaci 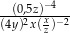 .
.
Udowodnij, że dla każdej liczby naturalnej  , liczba
, liczba 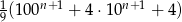 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Doprowadź wyrażenie ![[ ( √ -) 3 ( √ - ) 2] ( ) x√3y- 2 + -√-x- : x 14 + y14 y x3 x8 y3](https://img.zadania.info/zad/7702582/HzadT0x.gif) do najprostszej postaci.
do najprostszej postaci.
Uzasadnij, że jeśli 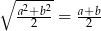 to
to 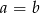 .
.
Wykaż, że jeśli  należy do zbioru liczb całkowitych, to
należy do zbioru liczb całkowitych, to 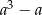 jest podzielne przez 3.
jest podzielne przez 3.
Dane są 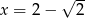 i
i 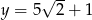 . Oblicz
. Oblicz 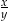 .
.

