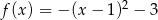Zestaw użytkownika nr 1970_2976
FUNKCJA KWADRATOWA ZALICZENIESuma punktów: 30
Jeżeli miejscami zerowymi funkcji kwadratowej są liczby 6 oraz -2, a wierzchołek paraboli będącej jej wykresem ma współrzędne  , to wzór tej funkcji można zapisać w postaci
, to wzór tej funkcji można zapisać w postaci
A) 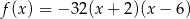
B) 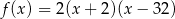
C) 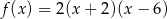
D) 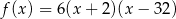
Największą wartość w przedziale 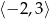 funkcja kwadratowa
funkcja kwadratowa 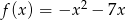 przyjmuje dla argumentu
przyjmuje dla argumentu
A) 3 B) -3,5 C) -2 D) 0
Zbiorem wartości funkcji kwadratowej 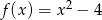 jest
jest
A) 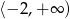 B)
B) 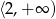 C)
C) 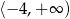 D)
D) 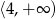
Jeżeli 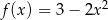 to funkcja
to funkcja 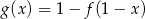 ma wzór
ma wzór
A) 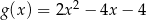
B) 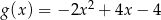
C) 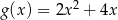
D) 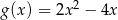
Funkcja 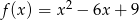 dla argumentu
dla argumentu 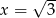 przyjmuje wartość
przyjmuje wartość
A) 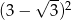 B) -36 C)
B) -36 C) 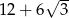 D)
D) 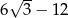
Dana jest funkcja
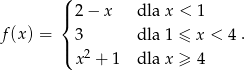
Wówczas
A) 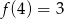 B)
B) 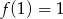 C)
C) 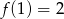 D)
D) 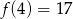
Osią symetrii paraboli będącej wykresem funkcji 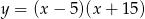 jest prosta o równaniu
jest prosta o równaniu
A) 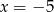 B)
B) 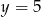 C)
C) 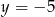 D)
D) 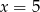
Wykres funkcji kwadratowej 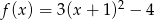 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 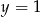 B)
B) 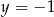 C)
C) 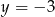 D)
D) 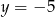
Dane są funkcje liniowe 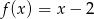 oraz
oraz 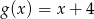 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 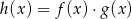 .
.
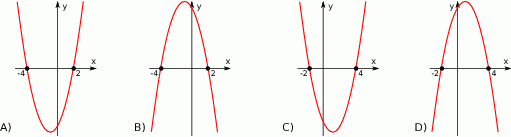
Gdy przesuniemy wykres funkcji 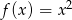 o 7 jednostek w lewo i 4 jednostki w dół, to otrzymamy wykres funkcji
o 7 jednostek w lewo i 4 jednostki w dół, to otrzymamy wykres funkcji
A) 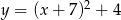 B)
B) 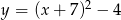 C)
C) 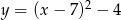 D)
D) 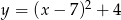
Wyznacz najmniejszą wartość funkcji 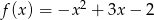 w przedziale
w przedziale 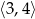 .
.
Wyznacz zbiór wartości funkcji 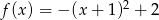 .
.
Określ zbiór wartości funkcji: 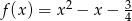 . Dla jakich argumentów funkcja przyjmuje wartości ujemne?
. Dla jakich argumentów funkcja przyjmuje wartości ujemne?
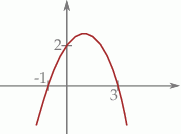
Na podstawie wykresu funkcji kwadratowej podaj jej wzór.
Napisz równanie osi symetrii wykresu funkcji 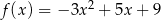 .
.
Suma trzech liczb rzeczywistych dodatnich jest równa 13. Druga liczba jest trzy razy większa od pierwszej. Wyznacz trzy liczby spełniające podane warunki tak, aby suma ich kwadratów była najmniejsza.
Liczbę 42 przedstaw w postaci sumy dwóch składników tak, by różnica ich kwadratów była równa 168.
Wskaż funkcję kwadratową rosnąca w przedziale 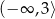 .
.
A) 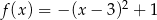
B) 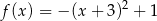
C) 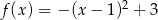
D)