/Szkoła średnia/Zadania maturalne
Geometria analityczna Zestaw zadań otwartych nr 197816
wygenerowany automatycznie w serwisie zadania.info poziom rozszerzony Czas pracy: 60 minut
Zadanie 1
(3 pkt)
W układzie współrzędnych są dane punkty 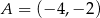 ,
, 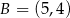 .
.
- Oblicz odległość punktu
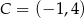 od prostej przechodzącej przez punkty
od prostej przechodzącej przez punkty 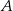 i
i 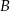 .
. - Uzasadnij, że jeśli
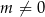 , to punkty
, to punkty 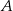 ,
, 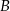 oraz punkt
oraz punkt 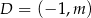 są wierzchołkami trójkąta.
są wierzchołkami trójkąta.
Zadanie 2
(3 pkt)
Dany jest okrąg 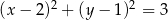 . Oblicz długości przekątnych rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę
. Oblicz długości przekątnych rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę 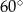 .
.
Zadanie 3
(4 pkt)
W trójkącie 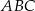 dane są:
dane są: 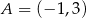 ,
, ![→ AB = [5,− 4]](https://img.zadania.info/zes/0197816/HzesT13x.gif) oraz
oraz ![→ BC = [2,6]](https://img.zadania.info/zes/0197816/HzesT14x.gif) . Trójkąt
. Trójkąt 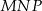 jest obrazem trójkąta
jest obrazem trójkąta 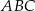 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 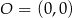 i skali
i skali 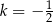 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 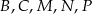 .
.
Zadanie 4
(5 pkt)
Punkt 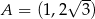 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 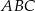 . Bok
. Bok 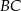 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 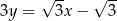 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 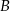 i
i 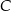 trójkąta.
trójkąta.
Zadanie 5
(5 pkt)
Z punktu 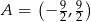 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 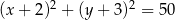 . Oblicz pole trójkąta
. Oblicz pole trójkąta 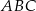 , gdzie
, gdzie 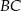 jest odcinkiem łączącym punkty styczności.
jest odcinkiem łączącym punkty styczności.

