Zestaw użytkownika nr 1986_2135
Egzamin 2012Zadania 229 Lutego 2012Czas pracy: 60 min.Suma punktów: 50
Na którym rysunku narysowano średnicę okręgu?

Wierzchołek 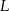 prostokąta przedstawionego na rysunku ma współrzędne
prostokąta przedstawionego na rysunku ma współrzędne
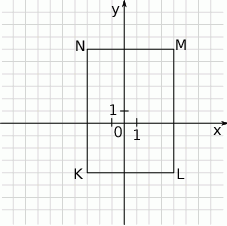
A) 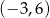 B)
B) 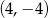 C)
C) 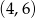 D)
D) 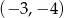
Figurami podobnymi są figury
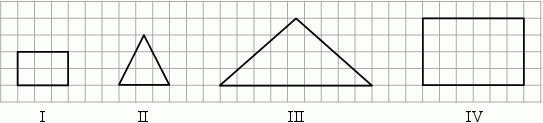
A) III i IV B) II i III C) I i IV D) I i II
Równość 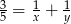 będzie prawdziwa, jeśli w miejsce
będzie prawdziwa, jeśli w miejsce  i
i 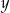 zostaną wpisane liczby
zostaną wpisane liczby
A) 10 i 2 B) 10 i 6 C) 6 i 4 D) 5 i 2
Oblicz pole trójkąta równoramiennego 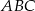 , w którym
, w którym 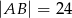 i
i 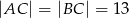 .
.
Sprawdź czy trójkąt jest prostokątny, jeżeli jego boki mają długości: 8 cm, 10 cm, 12 cm.
Wyznacz 155-tą cyfrę po przecinku rozwinięcia dziesiętnego liczby 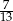 .
.
Średnia arytmetyczna liczb 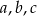 jest równa 15. Oblicz średnią arytmetyczną liczb
jest równa 15. Oblicz średnią arytmetyczną liczb 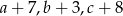 .
.
Zapoznaj się z rysunkiem przedstawiającym różne odcinki.
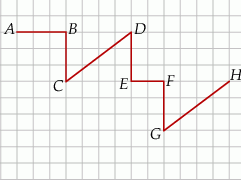
Uzupełnij zdania, korzystając z rysunku i podanych wyrazów. Zaznacz literę A lub B.
| A | prostopadłe |
| B | równoległe |
Odcinki 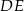 i i 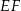 są są | A | B |
Odcinki 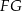 i i 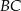 są są | A | B |
Odcinki 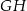 i i 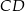 są są | A | B |
Rysunek przedstawia ostrosłup prosty.
Oceń, czy podane zdania są prawdziwe. Zaznacz TAK lub NIE.
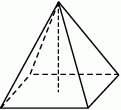
| Ściany boczne ostrosłupa są trójkątami prostokątnymi. | TAK | NIE |
| Liczba wszystkich krawędzi ostrosłupa jest parzysta. | TAK | NIE |
| Wszystkie ściany boczne ostrosłupa mają wspólny wierzchołek. | TAK | NIE |
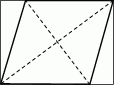
Paweł zamówił szybę w kształcie rombu o przekątnych 40 cm i 30 cm. Zaproponował szklarzowi, by wyciął romb z prostokątnego kawałka szyby, tak jak na rysunku. Jakie wymiary ma ten prostokątny kawałek szyby?
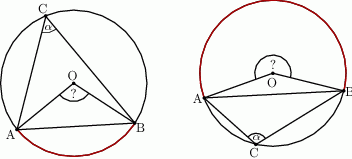
Oblicz miary kątów środkowych 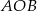 zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego
zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego 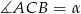 .
.
Punkty 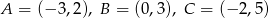 to wierzchołki trójkąta. Podaj, jakie są współrzędne wierzchołków trójkąta symetrycznego do trójkąta
to wierzchołki trójkąta. Podaj, jakie są współrzędne wierzchołków trójkąta symetrycznego do trójkąta 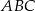 względem
względem
- osi
 ,
, - osi
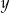 ,
, - punktu
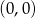 .
.
Punkt 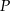 jest punktem przecięcia wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt
jest punktem przecięcia wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt 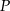 z wierzchołkiem trójkąta ma długość
z wierzchołkiem trójkąta ma długość 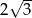 ?
?
W pewnej klasie liczba dziewcząt stanowi 60% liczby osób w tej klasie. Gdy 6 dziewcząt wyjechało na mecz siatkówki, w klasie pozostało tyle samo chłopców, ile dziewcząt. Oblicz, ile osób liczy ta klasa oraz ilu jest w niej chłopców.
Oblicz obwód czworokąta o wierzchołkach 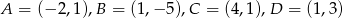 .
.
Graniastosłup prawidłowy czworokątny o krawędzi 4 cm i wysokości 3 cm przecięto płaszczyzną, która zawiera przekątne przeciwległych ścian bocznych. Jakie pole ma ten przekrój?

