/Szkoła średnia/Zadania maturalne
Stereometria Zestaw zadań otwartych nr 199069
wygenerowany automatycznie w serwisie zadania.info poziom rozszerzony Czas pracy: 60 minut
Objętość graniastosłupa prawidłowego trójkątnego jest równa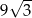 
, a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
W ostrosłup prawidłowy czworokątny wpisujemy graniastosłupy prawidłowe czworokątne w ten sposób, że dolna podstawa graniastosłupa zawiera się podstawie ostrosłupa, a każdy z wierzchołków górnej podstawy należy do jednej z krawędzi bocznych ostrosłupa. Wiedząc, że każda z krawędzi ostrosłupa ma długość 6, oblicz jaka jest maksymalna możliwa powierzchnia boczna graniastosłupa.
Odległość środka podstawy ostrosłupa prawidłowego czworokątnego od krawędzi bocznej równa się 
, a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się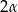 
. Oblicz wysokość ostrosłupa.
Trapez równoramienny o podstawach długości 14 cm i 26 cm oraz o wysokości 6 cm obraca się wokół swojej osi symetrii. Oblicz objętość otrzymanej bryły.
