Zestaw użytkownika nr 2032_7032

Zestaw użytkownika
nr 2032_7032

Zadanie 1

(5 pkt)

Rozwiąż równanie 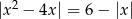2 |x − 4x | = 6− |x | .

Zadanie 2

(5 pkt)

Zbadaj liczbę rozwiązań równania 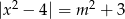2 2 |x − 4| = m + 3 w zależności od parametru .

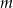Zadanie 3

(5 pkt)

Dla jakich wartości parametru 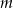układ równań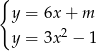 { y = 6x + m y = 3x 2 − 1

ma jedno rozwiązanie,
ma dwa rozwiązania.

Zadanie 4

(5 pkt)

Dla jakich wartości parametru 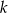wśród rozwiązań układu równań:

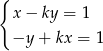
{ x− ky = 1 −y + kx = 1

jest para liczb 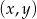(x,y ) spełniających warunek: x+ 4y ≤ 1 ?

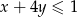Zadanie 5

(5 pkt)

Wyznacz te wartości parametru 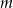, dla których nierówność 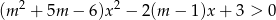(m 2 + 5m − 6)x2 − 2(m − 1 )x+ 3 > 0 jest prawdziwa dla każdego x ∈ R .

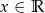Zadanie 6

(5 pkt)

Rozwiąż nierówność 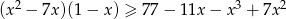2 3 2 (x − 7x )(1− x) ≥ 77 − 11x − x + 7x .

Zadanie 7

(5 pkt)

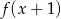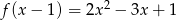Wyznacz f(x + 1 ) jeżeli 2 f(x − 1) = 2x − 3x + 1 .

Zadanie 8

(5 pkt)

Funkcja 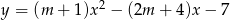2 y = (m + 1)x − (2m + 4)x− 7 jest malejąca w zbiorze 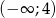(− ∞ ;4) i rosnąca w zbiorze 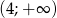(4;+ ∞ ) . Wyznacz parametr .

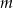Zadanie 9

(5 pkt)

Określ zbiór wartości i przedziały monotoniczności funkcji 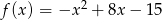2 f(x) = −x + 8x − 1 5 .

Zadanie 10

(5 pkt)

Podaj wartość wyrażenia 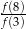f(8)- f(3) jeżeli 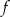jest funkcją kwadratową o miejscach zerowych 2 i 4.

Arkusz Wersja PDF