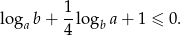Zestaw użytkownika nr 2058_7488
Funkcja wykładnicza i logarytmiczna
Zadanie 1
Wyznacz wszystkie wartości parametru 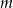 , dla których dziedziną funkcji
, dla których dziedziną funkcji
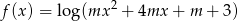
jest zbiór wszystkich liczb rzeczywistych.
Zadanie 2
Rozwiąż równanie ![1 log4(1 + log3[1 + log2(x + 3)]) = 2](https://img.zadania.info/zad/8382688/HzadT0x.gif) .
.
Zadanie 3
Rozwiąż równanie 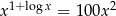 .
.
Zadanie 4
Rozwiąż nierówność 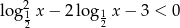 .
.
Zadanie 5
Rozwiąż nierówność 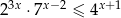 .
.
Zadanie 6
Rozwiąż równanie 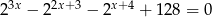 .
.
Zadanie 7
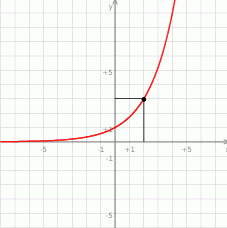
Na rysunku przedstawiony jest wykres funkcji wykładniczej 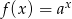 dla
dla 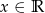 .
.
- Oblicz
 .
. - Narysuj wykres funkcji
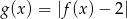 i podaj wszystkie wartości parametru
i podaj wszystkie wartości parametru 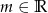 , dla których równanie
, dla których równanie 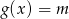 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
Zadanie 8
Dany jest wykres funkcji logarytmicznej 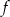 .
.
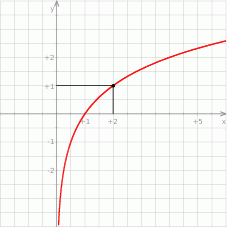
- Wyznacz wzór funkcji
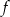 .
. - Narysuj wykres funkcji
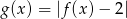 .
. - Odczytaj z rysunku zbiór argumentów, dla których wartości funkcji
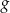 są nie mniejsze od wartości funkcji
są nie mniejsze od wartości funkcji 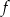 .
.
Zadanie 9
Wykaż, że jeżeli 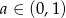 i
i 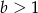 to prawdziwa jest nierówność
to prawdziwa jest nierówność