Poradnik stanowi uzupełnienie poradnika o zbiorach, więc radzimy zajrzeć tam w celu przypomnienia sobie najważniejszych definicji. Definicje Ustalmy zbiory 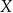 i
i 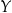 .
.
Relacją o dziedzinie 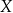 i przeciwdziedzinie
i przeciwdziedzinie 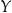 nazywamy dowolny podzbiór
nazywamy dowolny podzbiór 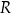 iloczynu kartezjańskiego
iloczynu kartezjańskiego 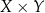 .
.
Iloczyn kartezjański 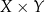 to zbiór par postaci
to zbiór par postaci 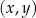 , gdzie
, gdzie 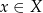 i
i  . Zatem wybranie podzbioru
. Zatem wybranie podzbioru  (ustanowienie relacji) polega na połączeniu w pary pewnych elementów zbioru
(ustanowienie relacji) polega na połączeniu w pary pewnych elementów zbioru 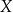 z elementami zbioru
z elementami zbioru 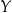 . Jeżeli elementy
. Jeżeli elementy  i
i 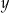 są w relacji
są w relacji 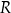 to piszemy
to piszemy 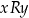 .
.
Poniższy diagram stanowi schematyczną ilustrację relacji między dwoma zbiorami skończonymi 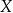 i
i 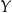 .
.
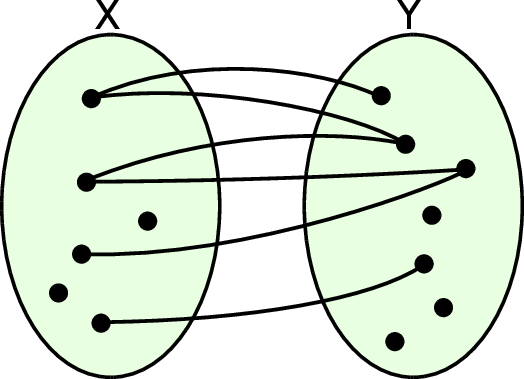
Jeżeli przez  oznaczymy zbiór wszystkich książek, a przez
oznaczymy zbiór wszystkich książek, a przez  zbiór wszystkich ludzi to w zbiorze
zbiór wszystkich ludzi to w zbiorze  mamy relację autorstwa, która łączy w pary książkę z jej autorami. Relacja ta jest dość skomplikowana, bo książki miewają wielu autorów, a autorzy często piszą wiele książek.
mamy relację autorstwa, która łączy w pary książkę z jej autorami. Relacja ta jest dość skomplikowana, bo książki miewają wielu autorów, a autorzy często piszą wiele książek.
Osoby interesujące się informatyką z pewnością spotkały się z pojęciem relacyjnej bazy danych. Jest to sposób na przechowywanie i organizację dużych ilości danych opierający się na tabelach, których kolumny połączone są relacjami.
Bardzo ważnym przykładem relacji są funkcje.
Relację  nazywamy funkcją jeżeli dla każdego
nazywamy funkcją jeżeli dla każdego 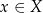 jest dokładnie jeden
jest dokładnie jeden  taki, że
taki, że 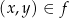 . Piszemy wtedy
. Piszemy wtedy 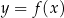 .
.
Zauważmy, że zgodnie z powyższą definicją funkcja jest zbiorem par postaci 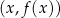 .
.
Używając języka diagramów o funkcjach myślimy jak o relacjach, w których z każdego elementu zbioru 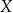 wychodzi dokładnie jedna strzałka.
wychodzi dokładnie jedna strzałka.
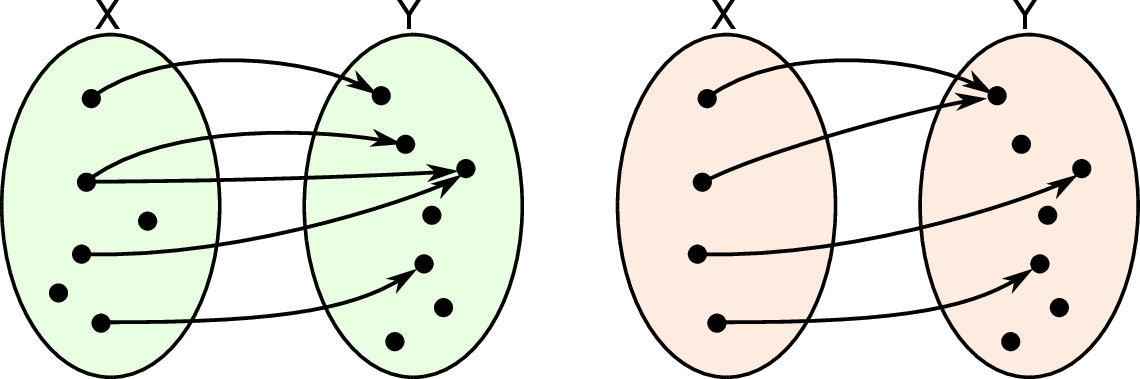
Relacja przedstawiona na lewym diagramie nie jest funkcją, bo są elementy, z których nie wychodzi żadna strzałka oraz takie, z których wychodzi więcej niż jedna strzałka. Relacja z prawego diagramu jest funkcją.
Funkcjom poświęcony jest osobny poradnik, w którym znajdziecie więcej informacji na ich temat. My natomiast skoncentrujemy się teraz na innej ciekawej sytuacji, mianowicie na przypadku  .
.
Relacją w zbiorze 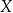 nazywamy dowolny podzbiór iloczynu kartezjańskiego
nazywamy dowolny podzbiór iloczynu kartezjańskiego 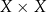 .
.
Wybranie podzbioru  oznacza ustanowienie relacji
oznacza ustanowienie relacji 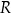 (związku) pomiędzy niektórymi elementami zbioru
(związku) pomiędzy niektórymi elementami zbioru 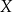 . Dokładniej,
. Dokładniej, 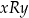 jeżeli
jeżeli 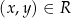 .
.
Dobrze znacie kilka relacji w zbiorze  . Np.:
. Np.: 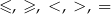 .
.
W tym przypadku relacje są podzbiorem zbioru  , czyli płaszczyzny. Możemy więc rysować wykresy relacji: zaznaczamy w układzie współrzędnych wszystkie punkty, z których składa się relacja.
, czyli płaszczyzny. Możemy więc rysować wykresy relacji: zaznaczamy w układzie współrzędnych wszystkie punkty, z których składa się relacja.

Na lewym diagramie naszkicowaliśmy wykres relacji „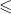 ”, a na prawym wykres relacji „
”, a na prawym wykres relacji „ ”.
”.
W zbiorze wszystkich ludzi mamy relację znajomości: osoba  jest w relacji z
jest w relacji z  jeżeli
jeżeli 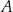 zna
zna 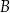 .
.
W zbiorze liczb naturalnych jest bardzo ważna relacja podzielności „ ”, tzn.
”, tzn. 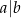 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy  dzieli
dzieli 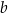 .
.
W zbiorze prostych na płaszczyźnie mamy relacje „ ” i „
” i „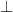 ”.
”.
W zbiorze wszystkich trójkątów na płaszczyźnie mamy relacje przystawania oraz podobieństwa.
Przyjęta przez nas definicja relacji jest bardzo ogólna i jak widzieliśmy podpada pod nią wiele różnych przykładów. Aby trochę tę sytuację uporządkować wyróżnia się różne cechy relacji. Relację 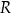 w zbiorze
w zbiorze  nazywamy:
nazywamy:
-
zwrotną jeżeli dla każdego
 mamy
mamy 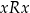 ;
; -
przechodnią jeżeli dla dowolnych
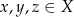 jeżeli
jeżeli 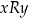 i
i 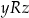 to
to 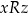 ;
; -
symetryczną jeżeli dla dowolnych
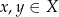 jeżeli
jeżeli 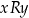 to
to 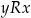 ;
; -
antysymetryczną jeżeli dla dowolnych
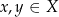 jeżeli
jeżeli 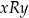 i
i 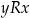 to
to 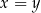 .
.
Relacje „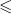 ” i „
” i „ ” są zwrotne, przechodnie i słabo antysymetryczne.
” są zwrotne, przechodnie i słabo antysymetryczne.
Relacja „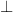 ” prostopadłości prostych na płaszczyźnie jest symetryczna.
” prostopadłości prostych na płaszczyźnie jest symetryczna.
Relacje porządku (nierówności) Jednym z powodów definiowania w zbiorze relacji jest chęć nadania mu dodatkowej struktury. Przykładem takiej struktury może być możliwość porównywania ze sobą elementów, czyli jakaś forma nierówności między elementami. Spróbujmy teraz sprecyzować co rozumiemy przez nierówność.
Relację 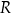 w zbiorze
w zbiorze  nazywamy częściowym porządkiem jeżeli jest zwrotna, przechodnia i antysymetryczna.
nazywamy częściowym porządkiem jeżeli jest zwrotna, przechodnia i antysymetryczna.
Warunki definiujące częściowy porządek to minimum, jakiego oczekujemy od (słabej) nierówności.
Relację będącą częściowym porządkiem często oznacza się symbolem „ ”. Warunki definiujące częściowy porządek wyglądają wtedy bardzo naturalnie: dla dowolnych
”. Warunki definiujące częściowy porządek wyglądają wtedy bardzo naturalnie: dla dowolnych 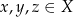
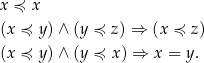
Relacja „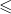 ” jest częściowym porządkiem w zbiorze
” jest częściowym porządkiem w zbiorze 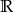 oraz w każdym jego podzbiorze.
oraz w każdym jego podzbiorze.
W zbiorze 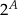 składającym się ze wszystkich podzbiorów zbioru
składającym się ze wszystkich podzbiorów zbioru 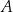 relacją częściowego porządku jest inkluzja „
relacją częściowego porządku jest inkluzja „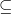 ”.
”.
Spróbujmy się zastanowić jak porównywać ze sobą punkty płaszczyzny.
Pierwszą naiwną próbą mogłoby być porównywanie drugich współrzędnych, czyli relacja 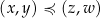 jeżeli
jeżeli 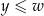 . Jak łatwo sprawdzić (zróbcie to!) relacja ta nie jest jednak antysymetryczna, więc nie jest to częściowy porządek.
. Jak łatwo sprawdzić (zróbcie to!) relacja ta nie jest jednak antysymetryczna, więc nie jest to częściowy porządek.
Mówiąc poglądowo, relacja ta jest zła, bo jest mnóstwo punktów, które z punktu widzenia tej nierówności są równe (punkty leżące na poziomych prostych).
Jeszcze jedno podejście do uporządkowania płaszczyzny: zamiast porównywać drugie współrzędne, porównujmy obie współrzędne na raz, tzn. przyjmijmy 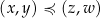 jeżeli jednocześnie
jeżeli jednocześnie 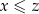 i
i 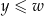 . Łatwo sprawdzić, że jest to relacja częściowego porządku.
. Łatwo sprawdzić, że jest to relacja częściowego porządku.
Jak już pisaliśmy warunki definiujące częściowy porządek to minimum, jakiego oczekujemy od nierówności, jednak często jest to minimum niewystarczające. Dużym problemem w przypadku częściowego porządku jest to, że zazwyczaj są elementy, których nie możemy ze sobą porównać.
Relację „ ” w zbiorze
” w zbiorze 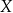 nazywamy liniowym porządkiem jeżeli jest częściowym porządkiem oraz dla dowolnych
nazywamy liniowym porządkiem jeżeli jest częściowym porządkiem oraz dla dowolnych 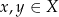
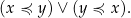
Liniowy porządek jest to więc częściowy porządek, w którym każde dwa elementy można ze sobą porównać.
Relacja inkluzji 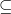 jest częściowym porządkiem, ale nie jest liniowym porządkiem, bo np. nie można przy jej pomocy porównać zbiorów
jest częściowym porządkiem, ale nie jest liniowym porządkiem, bo np. nie można przy jej pomocy porównać zbiorów 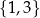 i
i  .
.
Zwykła nierówność „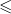 ” jest liniowym porządkiem w zbiorze
” jest liniowym porządkiem w zbiorze  .
.
Widzieliśmy już, że nierówność na płaszczyźnie zdefiniowana warunkiem
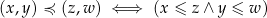
jest częściowym porządkiem. Nie jest to jednak linowy porządek, bo przy jego pomocy nie da się porównać np. punktów 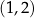 i
i 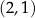 .
.
Czy na płaszczyźnie da się wprowadzić liniowy porządek? Tak, jest to np. porządek leksykograficzny zdefiniowany warunkiem

(porównujemy przede wszystkim pierwsze współrzędne, a tylko gdy są równe patrzymy na drugie). Oczywiście właśnie w ten sposób szukacie haseł w słowniku.
Relacje równoważności i klasy abstrakcji
Relację, która jest jednocześnie zwrotna, przechodnia i symetryczna nazywamy relacją równoważności.
W tym przypadku relację często oznaczamy symbolem „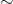 ” lub „
” lub „ ”.
”.
Tak jak relacja częściowego porządku stanowi uogólnienie nierówności, relacja równoważności stanowi uogólnienie równości. Różnicę między tymi dwoma pojęciami widać w definicji: mamy symetrię zamiast antysymetrii.
Relacja równoległości prostych na płaszczyźnie jest relacją równoważności.
Relacje przystawania i podobieństwa są relacjami równoważności.
Relacja równoważności ma działać jak uogólnienie równości, tzn. obiekty równoważne mają być „takie same z jakiegoś punktu widzenia”. Tak jest w podanych wyżej przykładach: w przypadku równoległości prostych relacja ustala równoważność prostych, które mają ten sam kierunek, a w przypadku podobieństwa trójkątów relacja utożsamia trójkąty, które są podobne. Przy takim rozumieniu równoważności podane wymagania, czyli zwrotność, symetria i przechodniość są dość naturalne.
Ważną cechą relacji równoważności jest to, że dzieli ona zbiór 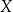 na rozłączne podzbiory (zwane klasami abstrakcji) składające się z elementów, które są ze sobą w relacji. Zbiór składający się z klas abstrakcji oznaczamy symbolem
na rozłączne podzbiory (zwane klasami abstrakcji) składające się z elementów, które są ze sobą w relacji. Zbiór składający się z klas abstrakcji oznaczamy symbolem 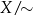 .
.
O zbiorze  myślimy jak o zbiorze mniejszym od
myślimy jak o zbiorze mniejszym od  . Tak jest, bo tworząc
. Tak jest, bo tworząc 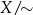 sklejamy wszystkie elementy zbioru
sklejamy wszystkie elementy zbioru 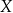 będące w relacji w jeden element zbioru
będące w relacji w jeden element zbioru  .
.
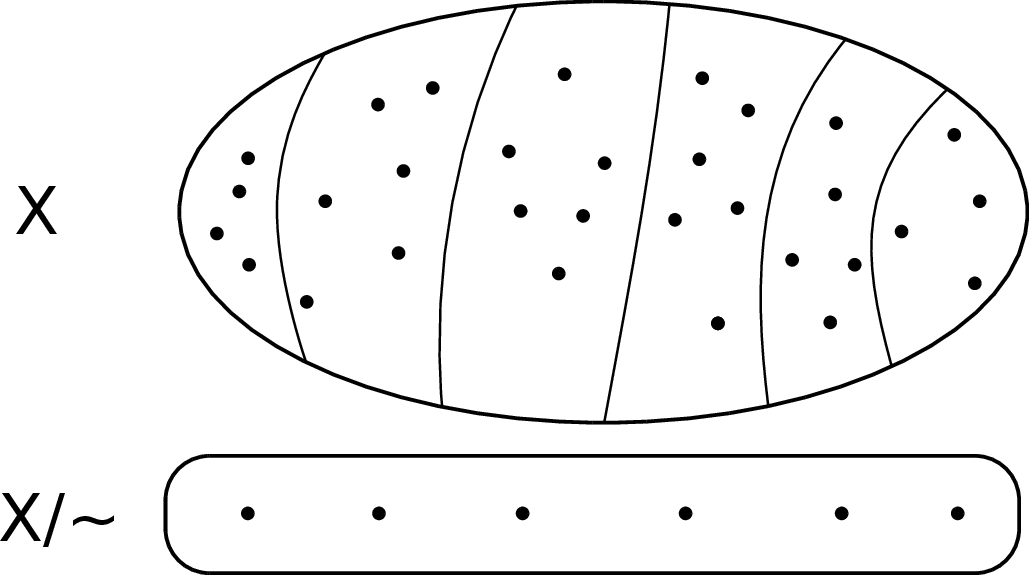
Powyższy schematyczny rysunek przedstawia zbiór 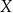 podzielony na 6 klas abstrakcji pewnej relacji równoważności „
podzielony na 6 klas abstrakcji pewnej relacji równoważności „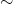 ”. W takiej sytuacji zbiór
”. W takiej sytuacji zbiór 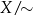 składa się z sześciu elementów.
składa się z sześciu elementów.
Relacja „ten sam wzrost w cm” jest relacją równoważności w zbiorze wszystkich ludzi. Podobne relacje to np. „ten sam kolor oczu”, „wspólny pradziadek”, „to samo pierwsze imię”, „ten sam dzień urodzenia”. Każda z tych relacji dokonuje podziału zbioru wszystkich ludzi na klasy abstrakcji ze względu na interesującą nas cechę.
Jeżeli „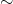 ” jest relacją „
” jest relacją „ ” równoległości prostych na płaszczyźnie, to zbiory elementów będących w relacji (czyli klasy abstrakcji tej relacji) to po prostu zbiory prostych, które są wzajemnie równoległe. Zbiorów tych jest tyle, ile możliwych kierunków na płaszczyźnie. Dlatego o zbiorze
” równoległości prostych na płaszczyźnie, to zbiory elementów będących w relacji (czyli klasy abstrakcji tej relacji) to po prostu zbiory prostych, które są wzajemnie równoległe. Zbiorów tych jest tyle, ile możliwych kierunków na płaszczyźnie. Dlatego o zbiorze 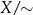 myślimy jak o zbiorze kierunków.
myślimy jak o zbiorze kierunków.
Spróbujmy na poprzedni przykład popatrzeć z drugiej strony. Zastanówmy się co to jest kierunek prostej? Trudno powiedzieć, co to dokładnie jest, ale wiemy, że niektóre proste mają ten sam kierunek, np. 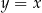 ,
, 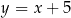 ,
, 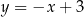 . I taki właśnie jest pomysł na definicję kierunku: jeden kierunek to coś, co mają wspólnego ze sobą proste
. I taki właśnie jest pomysł na definicję kierunku: jeden kierunek to coś, co mają wspólnego ze sobą proste  ,
, 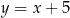 ,
, 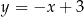 i wszystkie inne o współczynniku kierunkowym
i wszystkie inne o współczynniku kierunkowym  , inny kierunek to coś, co mają ze sobą wspólnego wszystkie proste o współczynniku
, inny kierunek to coś, co mają ze sobą wspólnego wszystkie proste o współczynniku  itd. Jeżeli teraz popatrzycie na opis zbioru
itd. Jeżeli teraz popatrzycie na opis zbioru 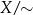 powyżej to powinno być jasne, że jest to sposób na precyzyjną definicję zbioru kierunków na płaszczyźnie.
powyżej to powinno być jasne, że jest to sposób na precyzyjną definicję zbioru kierunków na płaszczyźnie.
Przykład ten jest dość abstrakcyjny, ale dokładnie taka jest rola relacji równoważności i klas abstrakcji: pozwalają one precyzyjnie definiować abstrakcyjne pojęcia (kierunek w tym przypadku).
Jeżeli 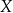 jest zbiorem trójkątów na płaszczyźnie, a „
jest zbiorem trójkątów na płaszczyźnie, a „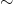 ” relacją podobieństwa, to jak wyobrazić sobie zbiór
” relacją podobieństwa, to jak wyobrazić sobie zbiór  ? Tworząc zbiór
? Tworząc zbiór 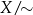 utożsamiamy ze sobą wszystkie trójkąty podobne, więc o zbiorze
utożsamiamy ze sobą wszystkie trójkąty podobne, więc o zbiorze 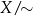 możemy myśleć jak o zbiorze wszystkich możliwych kształtów trójkątów. Np. trójkątowi równobocznemu odpowiada dokładnie jeden element zbioru
możemy myśleć jak o zbiorze wszystkich możliwych kształtów trójkątów. Np. trójkątowi równobocznemu odpowiada dokładnie jeden element zbioru  pomimo, że w zbiorze
pomimo, że w zbiorze 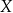 (na płaszczyźnie) jest nieskończenie wiele trójkątów równobocznych.
(na płaszczyźnie) jest nieskończenie wiele trójkątów równobocznych.
Gdybyśmy zamiast podobieństwa wzięli relację przystawania, to zbiór 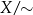 byłby zbiorem wszystkich możliwych kształtów z uwzględnieniem rozmiaru.
byłby zbiorem wszystkich możliwych kształtów z uwzględnieniem rozmiaru.
Ustalmy liczbę naturalną 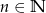 . W zbiorze liczb całkowitych
. W zbiorze liczb całkowitych  wprowadzamy relację „
wprowadzamy relację „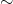 ” wzorem
” wzorem
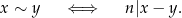
Mówiąc po ludzku: dwie liczby są w relacji wtedy i tylko wtedy, gdy dają tę samą resztę z dzielenia przez  . Zbiór
. Zbiór 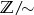 składa się
składa się  elementów, które możemy wypisać:
elementów, które możemy wypisać:
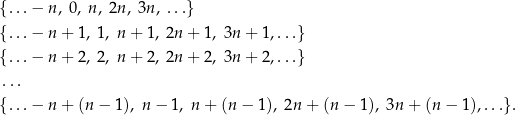
Zbiór 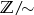 oznaczamy symbolem
oznaczamy symbolem 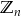 i jest to zbiór reszt z dzielenia przez
i jest to zbiór reszt z dzielenia przez  .
.
Jeżeli przejrzycie swoje podręczniki do matematyki to okaże się, że nie znajdziecie w nich definicji liczb wymiernych. Tak jest, bo definicja ta wymaga użycia relacji równoważności. Mówiąc dokładniej, liczb wymiernych nie można zdefiniować jako napisów postaci 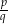 , gdzie
, gdzie  , bo przecież każda liczba wymierna może być w ten sposób napisana na nieskończenie wiele różnych sposobów. Np. czym jest
, bo przecież każda liczba wymierna może być w ten sposób napisana na nieskończenie wiele różnych sposobów. Np. czym jest  ? Napisem
? Napisem  ? A może jednym z napisów
? A może jednym z napisów
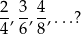
Problem w tym przypadku jest podobny jak z definicją kierunku na płaszczyźnie: to co chcemy zdefiniować jest abstrakcyjne: ma to być „połowa całości”, a nie ten czy inny napis. Jak w takim razie zdefiniować połowę? – skoro jest to cecha wspólna wszystkich powyższych ułamków, to definiujemy  jako wszystkie te ułamki na raz.
jako wszystkie te ułamki na raz.
Mówiąc bardziej precyzyjnie, w zbiorze 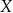 napisów postaci
napisów postaci  , gdzie
, gdzie 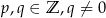 (jeżeli ktoś się zastanawia co to jest „zbiór napisów”, to jest to zbiór par
(jeżeli ktoś się zastanawia co to jest „zbiór napisów”, to jest to zbiór par 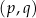 pisanych w taki oryginalny sposób) wprowadzamy relację „
pisanych w taki oryginalny sposób) wprowadzamy relację „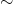 ” w następujący sposób: napisy
” w następujący sposób: napisy 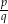 i
i 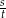 są w relacji „
są w relacji „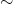 ” wtedy i tylko wtedy, gdy
” wtedy i tylko wtedy, gdy 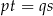 (jest to znany nam dobrze warunek równości ułamków). Można teraz sprawdzić, że „
(jest to znany nam dobrze warunek równości ułamków). Można teraz sprawdzić, że „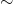 ” jest relacją równoważności oraz z definicji
” jest relacją równoważności oraz z definicji 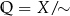 .
.
W tym miejscu powinniście już mniej więcej kojarzyć czym są klasy abstrakcji, więc możemy sobie pozwolić na małe porządki w notacji. Wiemy, że każdemu elementowi 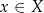 odpowiada element zbioru
odpowiada element zbioru 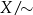 (jego klasa abstrakcji). Element ten oznaczamy symbolem
(jego klasa abstrakcji). Element ten oznaczamy symbolem ![[x ]∼](https://img.zadania.info/por/0020710/HporT164x.png) lub krótko
lub krótko ![[x]](https://img.zadania.info/por/0020710/HporT165x.png) . Zbiór
. Zbiór ![[x ]](https://img.zadania.info/por/0020710/HporT166x.png) jest więc zbiorem wszystkich elementów zbioru
jest więc zbiorem wszystkich elementów zbioru 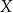 , które są w relacji z
, które są w relacji z  . W takiej sytuacji mówimy, że
. W takiej sytuacji mówimy, że  jest reprezentantem klasy abstrakcji
jest reprezentantem klasy abstrakcji ![[x]](https://img.zadania.info/por/0020710/HporT170x.png) . Oczywiście klasa abstrakcji może mieć wiele różnych reprezentantów, jeżeli np.
. Oczywiście klasa abstrakcji może mieć wiele różnych reprezentantów, jeżeli np. 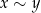 to
to ![[y] = [x]](https://img.zadania.info/por/0020710/HporT172x.png) , więc
, więc 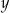 też jest reprezentantem klasy
też jest reprezentantem klasy ![[x ] = [y ]](https://img.zadania.info/por/0020710/HporT174x.png) .
.
Jeżeli „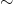 ” jest relacją równoległości prostych na płaszczyźnie to klasa
” jest relacją równoległości prostych na płaszczyźnie to klasa ![[y = 3x+ 1]](https://img.zadania.info/por/0020710/HporT176x.png) oznacza zbiór wszystkich prostych na płaszczyźnie ze współczynnikiem kierunkowym
oznacza zbiór wszystkich prostych na płaszczyźnie ze współczynnikiem kierunkowym 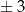 . Oczywiście ten sam zbiór możemy zapisać na wiele różnych sposobów, np.
. Oczywiście ten sam zbiór możemy zapisać na wiele różnych sposobów, np.
![[y = 3x + 1] = [y = − 3x− 1] = [y = 3x + 5].](https://img.zadania.info/por/0020710/HporT178x.png)
Każda z prostych 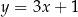 ,
, 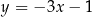 ,
, 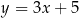 jest reprezentantem powyższej klasy abstrakcji (kierunku).
jest reprezentantem powyższej klasy abstrakcji (kierunku).
Ciągłe odróżnianie elementów od klas abstrakcji jest niewygodne, więc bardzo często pomijamy nawiasy ![[]](https://img.zadania.info/por/0020710/HporT182x.png) i piszemy
i piszemy  zamiast
zamiast ![[x]](https://img.zadania.info/por/0020710/HporT184x.png) (choć są to dwie różne rzeczy).
(choć są to dwie różne rzeczy).
Definiując liczby wymierne zdefiniowaliśmy „połowę” jako zbiór wszystkich ułamków postaci
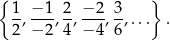
Formalnie „połowę” powinniśmy więc oznaczać jednym z symboli: ![[ ] 12](https://img.zadania.info/por/0020710/HporT186x.png) ,
, ![[3] 6 ,...](https://img.zadania.info/por/0020710/HporT187x.png) . Tak jednak nie robimy i piszemy krótko
. Tak jednak nie robimy i piszemy krótko 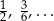 Zapis
Zapis 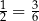 należy więc rozumieć jako skrót zapisu
należy więc rozumieć jako skrót zapisu ![[ ] 1 = [ 3] 2 6](https://img.zadania.info/por/0020710/HporT190x.png) .
.
W pewnym sensie jest to duże osiągnięcie matematyki, że możemy posługiwać się symbolami ułamków nie wiedząc nawet co one oznaczają. .
Formalnie zbiór 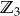 składa się z trzech elementów
składa się z trzech elementów
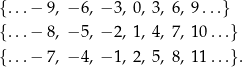
Napisy ![[− 3],[1],[8]](https://img.zadania.info/por/0020710/HporT193x.png) są jednak niewygodne, więc wolelibyśmy pisać po prostu
są jednak niewygodne, więc wolelibyśmy pisać po prostu 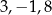 . Jest z tym jednak kłopot, bo np. napis
. Jest z tym jednak kłopot, bo np. napis ![[− 5] = [7]](https://img.zadania.info/por/0020710/HporT195x.png) (który oznacza po prostu, że obie liczby dają tę samą resztę z dzielenia przez 3) zamienia się na
(który oznacza po prostu, że obie liczby dają tę samą resztę z dzielenia przez 3) zamienia się na 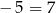 , co nie wygląda zbyt dobrze. Z tego powodu używa się specjalnej notacji: zamiast
, co nie wygląda zbyt dobrze. Z tego powodu używa się specjalnej notacji: zamiast ![[− 5] = [7 ]](https://img.zadania.info/por/0020710/HporT197x.png) piszemy
piszemy
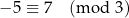
(czytamy 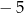 przystaje do 7 modulo 3). Czasami pisze się też krótko
przystaje do 7 modulo 3). Czasami pisze się też krótko  .
.

