Zestaw użytkownika nr 2075_1986
Wielomiany Super trudne27 Lutego 2011Czas pracy: 210 min.Suma punktów: 200
Dany jest wielomian 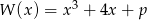 , gdzie
, gdzie 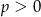 jest liczbą pierwszą. Znajdź
jest liczbą pierwszą. Znajdź 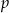 wiedząc, że
wiedząc, że 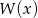 ma pierwiastek całkowity.
ma pierwiastek całkowity.
Liczba 2 jest miejscem zerowym wielomianu 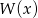 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 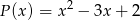 jeśli wiadomo, że w wyniku dzielenia wielomianu
jeśli wiadomo, że w wyniku dzielenia wielomianu 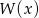 przez dwumian
przez dwumian 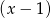 otrzymujemy resztę 5.
otrzymujemy resztę 5.
Reszta z dzielenia wielomianu 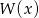 przez dwumian
przez dwumian 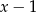 jest równa 1, zaś reszta z dzielenia tego wielomianu przez
jest równa 1, zaś reszta z dzielenia tego wielomianu przez 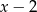 jest równa 4. Wyznacz resztę z dzielenia wielomianu
jest równa 4. Wyznacz resztę z dzielenia wielomianu 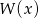 przez wielomian
przez wielomian 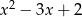 .
.
Przedstaw wielomian 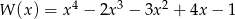 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
Dana jest funkcja 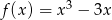 dla
dla 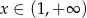 . Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale
. Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale 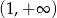 .
.
Wyznacz zbiór wartości funkcji 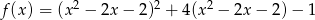 .
.
Oblicz najmniejszą wartość wielomianu 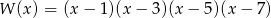 .
.
Rozłóż na czynniki drugiego stopnia wielomian 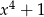 .
.
Wielomian 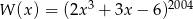 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 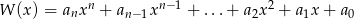 . Oblicz sumę
. Oblicz sumę 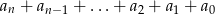 .
.
Uzasadnij, że dla każdej liczby naturalnej  wartość wielomianu
wartość wielomianu 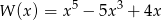 jest liczbą podzielną przez 120.
jest liczbą podzielną przez 120.
Wykaż, że jeżeli wielomian 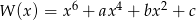 jest podzielny przez trójmian
jest podzielny przez trójmian 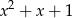 , to jest również podzielny przez trójmian
, to jest również podzielny przez trójmian 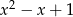 .
.
Wyznacz resztę z dzielenia wielomianu 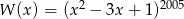 przez wielomian
przez wielomian 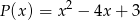 .
.
Wielomian 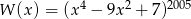 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 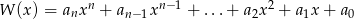 . Oblicz sumę
. Oblicz sumę 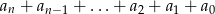 .
.
Liczba -7 jest miejscem zerowym 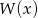 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 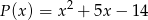 , jeśli wiadomo, że w wyniku dzielenia wielomianu
, jeśli wiadomo, że w wyniku dzielenia wielomianu 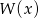 przez dwumian
przez dwumian 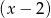 otrzymujemy resztę 18.
otrzymujemy resztę 18.
Wykaż, że wielomian 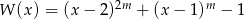 jest podzielny przez wielomian
jest podzielny przez wielomian 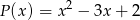 dla każdego
dla każdego 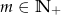 .
.
Dany jest wielomian 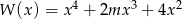 z parametrem
z parametrem 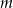 .
.
- Wiedząc, że wykres tego wielomianu jest symetryczny względem prostej
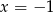 , wyznacz
, wyznacz 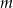 .
. - Dla wyznaczonej wartości parametru
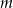 uzasadnij, że nierówność
uzasadnij, że nierówność 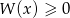 jest spełniona przez każdą liczbę rzeczywistą
jest spełniona przez każdą liczbę rzeczywistą 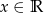 .
.
W wyniku jakiego przekształcenia (lub przekształceń) wykresu funkcji 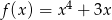 można otrzymać wykres funkcji
można otrzymać wykres funkcji 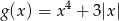 , jeżeli
, jeżeli
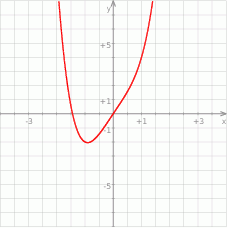 ;
; 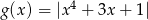 ;
; 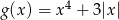 ?
?
Wykres funkcji 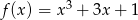 przekształcono w symetrii względem prostej
przekształcono w symetrii względem prostej 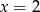 i otrzymano wykres funkcji
i otrzymano wykres funkcji 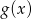 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 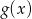 .
.
Dany jest wielomian 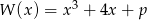 , gdzie
, gdzie 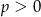 jest liczbą pierwszą. Znajdź
jest liczbą pierwszą. Znajdź 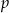 wiedząc, że
wiedząc, że 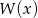 ma pierwiastek całkowity.
ma pierwiastek całkowity.
Liczby 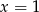 i
i 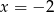 są pierwiastkami wielomianu
są pierwiastkami wielomianu 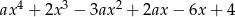 . Wiedząc, że wielomian ten jest kwadratem wielomianu stopnia 2, oblicz
. Wiedząc, że wielomian ten jest kwadratem wielomianu stopnia 2, oblicz  .
.
Wielomian 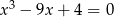 ma 3 pierwiastki rzeczywiste.
ma 3 pierwiastki rzeczywiste.
- Oblicz sumę odwrotności tych pierwiastków.
- Ustal, ile jest pierwiastków dodatnich.
- Oblicz odwrotność sumy kwadratów pierwiastków.
- Oblicz sumę kwadratów odwrotności tych pierwiastków.
Znajdź wielomian o współczynnikach całkowitych, którego pierwiastkiem jest liczba 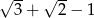 .
.
Wielomian 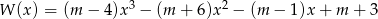 jest podzielny przez dwumian
jest podzielny przez dwumian 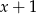 . Dla jakich wartości parametru
. Dla jakich wartości parametru 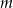 wielomian
wielomian 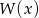 ma dokładnie dwa pierwiastki?
ma dokładnie dwa pierwiastki?
Dla jakich wartości parametru 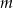 wielomian
wielomian 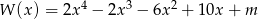 ma pierwiastek trzykrotny?
ma pierwiastek trzykrotny?
Wiedząc, że suma kwadratów pierwiastków równania
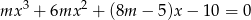
jest równa 30, wyznacz 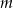 .
.
Rozważmy równanie 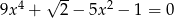 .
.
- Uzasadnij, że równanie to ma 4 pierwiastki.
- Oblicz sumę szóstych potęg wszystkich pierwiastków tego równania.
Dla jakich wartości parametru 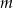 równanie
równanie ![2 2 (x − m ) [m(x − m ) − m − 1]+ 1 = 0](https://img.zadania.info/zad/3650840/HzadT1x.gif) ma więcej pierwiastków dodatnich niż ujemnych?
ma więcej pierwiastków dodatnich niż ujemnych?
Wyznacz współczynniki  i
i 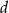 wielomianu
wielomianu 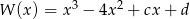 wiedząc, że liczba 1 jest dwukrotnym pierwiastkiem wielomianu
wiedząc, że liczba 1 jest dwukrotnym pierwiastkiem wielomianu 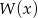 .
.
Udowodnij, że jeżeli wielomian 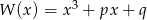 ma trzy pierwiastki, to
ma trzy pierwiastki, to 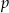 jest liczbą ujemną.
jest liczbą ujemną.
Dla jakich wartości parametru 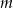 równanie
równanie 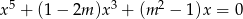 ma
ma
- pięć pierwiastków;
- dokładnie 3 pierwiastki;
- tylko jeden pierwiastek?
Dla jakich wartości parametru 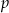 wielomian
wielomian 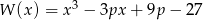 ma trzy różne pierwiastki rzeczywiste?
ma trzy różne pierwiastki rzeczywiste?
Wyznacz wszystkie wartości parametru 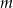 , dla których równanie
, dla których równanie
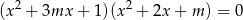
ma cztery różne pierwiastki, których suma sześcianów jest równa 4.
Wykaż, że jeżeli wielomian 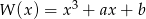 ma pierwiastek dwukrotny, to
ma pierwiastek dwukrotny, to 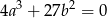 .
.
Wyznacz te wartości parametru 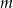 , dla których równanie
, dla których równanie 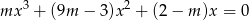 ma co najmniej jedno rozwiązanie dodatnie.
ma co najmniej jedno rozwiązanie dodatnie.
Wyznacz wartości parametrów  i
i 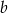 dla których jedynymi rozwiązaniami równania
dla których jedynymi rozwiązaniami równania
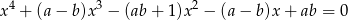
są liczby 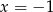 i
i 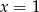 .
.
Wykaż, że równanie 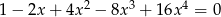 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
Dla jakich wartości parametru 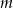 zbiór rozwiązań równania
zbiór rozwiązań równania 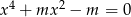 jest dwuelementowy?
jest dwuelementowy?
Wyznacz wartość parametru 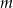 , dla którego równanie
, dla którego równanie
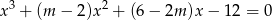
ma trzy pierwiastki 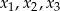 spełniające warunki
spełniające warunki 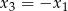 oraz
oraz 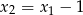 .
.
Dla jakich wartości parametru 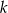 nierówność
nierówność 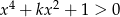 jest prawdziwa dla każdego
jest prawdziwa dla każdego 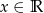 ?
?
Wyznacz wszystkie wartości parametrów 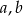 , dla których nierówność
, dla których nierówność
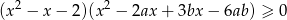
jest spełniona przez każdą liczbę rzeczywistą.

