Zestaw użytkownika nr 2080_5075

MATURA 2011Sprawdzian maturalny4 Marca 2011Czas pracy: 60 min.Suma punktów: 25

Zadanie 1

(5 pkt)

Rozwiąż nierówność 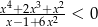x4+-2x3+x-2 x− 1+ 6x2 < 0 .

Zadanie 2

(5 pkt)

Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 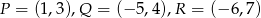P = (1,3),Q = (− 5,4),R = (− 6,7) .

Zadanie 3

(5 pkt)

Określ liczbę pierwiastków równania 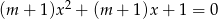2 (m + 1 )x + (m + 1)x + 1 = 0 w zależności od wartości parametru 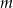, a następnie naszkicuj wykres funkcji:

( |{ x1 + x2 gdy dane równanie ma dwa pierwiastki x1 i x2, f(m ) = |( 2x0 gdy dane równanie ma jeden pierwiastek x 0, 3− m gdy dane równanie nie ma pierwiastków .

Zadanie 4

(5 pkt)

Na rysunku przedstawiony jest wykres funkcji 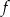określonej wzorem 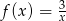f (x) = 3x dla x ⁄= 0 .

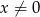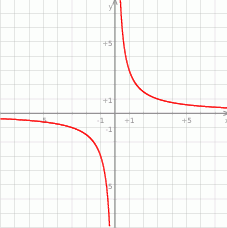
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 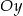. Otrzymano w ten sposób wykres funkcji 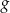o wzorze 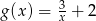g(x) = 3x + 2 dla x ⁄= 0 .

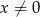Narysuj wykres funkcji .
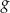Oblicz największą wartość funkcji 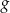w przedziale .
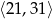Podaj, o ile jednostek wzdłuż osi 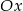należy przesunąć wykres funkcji 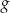, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.

Zadanie 5

(5 pkt)

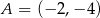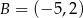Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach A = (− 2,− 4) oraz B = (− 5,2) . Jedno z jego ramion zawiera się w prostej o równaniu 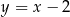y = x − 2 . Oblicz współrzędne trzeciego wierzchołka trójkąta.

Rozwiąż on-line Arkusz Wersja PDF