Zestaw użytkownika nr 2158_3826

Zestaw użytkownika
nr 2158_3826

Zadanie 1

Wyznacz najmniejszą i największą wartość funkcji 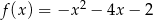2 f(x) = −x − 4x− 2 w przedziale ⟨− 2;2 ⟩ .

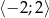Zadanie 2

Wyznacz wszystkie całkowite wartości 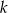, dla których funkcja 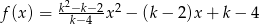2 f (x) = k-−k−k−42-x2 − (k− 2 )x+ k− 4 osiąga minimum i ma dwa różne miejsca zerowe.

Zadanie 3

Jednym z miejsc zerowych funkcji kwadratowej 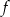jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to 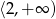⟨2 ,+∞ ) . Największa wartość funkcji 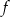w przedziale 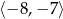⟨− 8,− 7⟩ jest równa 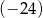(− 24) . Wyznacz wzór funkcji 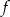i narysuj jej wykres.

Zadanie 4

Pierwiastkami trójmianu kwadratowego 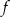o współczynniku -3 przy najwyższej potędze są liczby 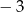x1 = − 6,x2 = 4 . Oblicz f(− 10 ) .

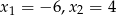Zadanie 5

Dla każdej liczby rzeczywistej 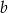równanie 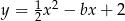1 2 y = 2x − bx + 2 opisuje pewną parabolę. Wyznacz wszystkie wartości parametru 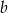, dla których wierzchołek paraboli leży nad osią .

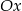Zadanie 6

Dany jest wykres funkcji kwadratowej 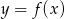y = f(x )

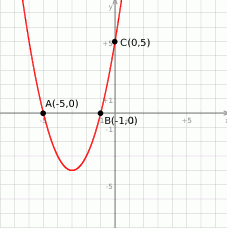
Korzystając z danych na wykresie wyznacz wzór funkcji 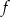w postaci ogólnej.
Oblicz współrzędne wierzchołka paraboli.
Podaj zbiór rozwiązań nierówności .

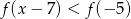Zadanie 7

Suma kwadratów trzech kolejnych ujemnych liczb całkowitych parzystych jest równa 116. Wyznacz te liczby.
Wyznacz takie trzy kolejne liczby całkowite parzyste, których suma kwadratów jest najmniejsza z możliwych.

Arkusz Wersja PDF