Zestaw użytkownika nr 2160_1871
Zestaw użytkownika
nr 2160_1871
Wykaż, że prosta 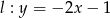 jest styczna do okręgu
jest styczna do okręgu 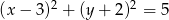 .
.
Wyznacz odległość punktu 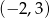 od prostej o równaniu
od prostej o równaniu 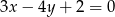 .
.
W układzie współrzędnych na płaszczyźnie punkty 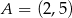 i
i 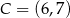 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 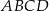 . Wyznacz równanie prostej
. Wyznacz równanie prostej 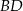 .
.
W układzie współrzędnych dane są dwa punkty: 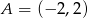 i
i 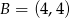 .
.
- Wyznacz równanie symetralnej odcinka
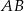 .
. - Prosta
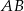 oraz prosta o równaniu
oraz prosta o równaniu 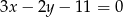 przecinają się w punkcie
przecinają się w punkcie 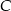 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 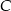 .
.
Dane są dwa przeciwległe wierzchołki kwadratu 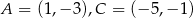 . Wyznacz obwód tego kwadratu.
. Wyznacz obwód tego kwadratu.
Dany jest jeden koniec odcinka 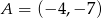 i jego środek
i jego środek 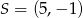 . Wyznacz współrzędne drugiego końca tego odcinka.
. Wyznacz współrzędne drugiego końca tego odcinka.
Określ wzajemne położenie prostych 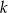 i
i 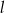 o równaniach
o równaniach
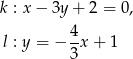
Określ wzajemne położenie okręgów 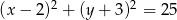 i
i 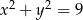 .
.
Oblicz pole i obwód trójkąta o wierzchołkach: 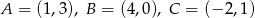 .
.
Dany jest równoległobok 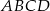 o wierzchołkach
o wierzchołkach 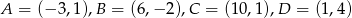 . Napisz równania prostych, w których zawarte są przekątne równoległoboku.
. Napisz równania prostych, w których zawarte są przekątne równoległoboku.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 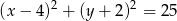 .
.
Oblicz odległość punktu 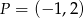 od prostej o równaniu
od prostej o równaniu 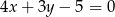 .
.
Napisz równanie okręgu o środku w punkcie 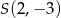 , stycznego do osi
, stycznego do osi 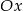 .
.
Wyznacz równanie prostej, która przecina oś 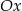 pod kątem
pod kątem 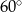 , a oś
, a oś 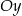 w punkcie
w punkcie 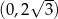 .
.
W układzie współrzędnych na płaszczyźnie zaznaczono punkty 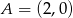 i
i 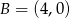 . Wyznacz wszystkie możliwe położenia punktu
. Wyznacz wszystkie możliwe położenia punktu 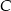 , dla których
, dla których 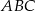 jest trójkątem równoramiennym o podstawie
jest trójkątem równoramiennym o podstawie 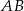 i polu równym 3.
i polu równym 3.
Prosta 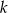 jest wykresem funkcji
jest wykresem funkcji 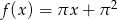 .
.
- Oblicz współrzędne punktu przecięcia prostej
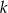 z wykresem funkcji
z wykresem funkcji 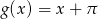 .
. - Znajdź równanie prostej przechodzącej przez punkt
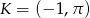 i równoległej do prostej
i równoległej do prostej 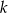 .
.
Określ wzajemne położenie okręgów: 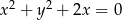 i
i 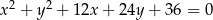 .
.
W kwadracie 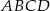 dane są wierzchołek
dane są wierzchołek 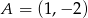 i środek symetrii
i środek symetrii 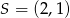 . Oblicz pole kwadratu
. Oblicz pole kwadratu 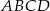 .
.
Wyznacz równanie prostej równoległej do prostej 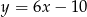 przechodzącej przez punkt
przechodzącej przez punkt 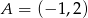 oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt
oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt 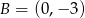 .
.
Napisz równanie prostej równoległej do prostej o równaniu 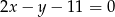 i przechodzącej przez punkt
i przechodzącej przez punkt 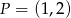 .
.
Wyznacz współrzędne punktów wspólnych prostej 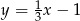 i okręgu
i okręgu 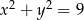 .
.
Wyznacz współrzędne wierzchołków trójkąta, którego boki zawarte są w prostych o równaniach 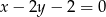 ,
, 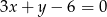 ,
, 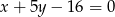 .
.

