Zestaw użytkownika nr 2186_1660

Zestaw użytkownika
nr 2186_1660

Zadanie 1

(5 pkt)

Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 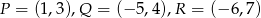P = (1,3),Q = (− 5,4),R = (− 6,7) .

Zadanie 2

(5 pkt)

Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.

Zadanie 3

(5 pkt)

Dany jest wielomian 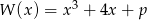3 W (x) = x + 4x + p , gdzie 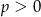p > 0 jest liczbą pierwszą. Znajdź 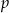wiedząc, że 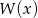W (x) ma pierwiastek całkowity.

Zadanie 4

(5 pkt)

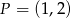Dla jakich wartości parametru odległość punktu P = (1,2) od prostej 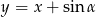y = x+ sin α jest mniejsza lub równa 1√2- .

Zadanie 5

(5 pkt)

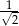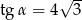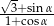Wiedząc, że jest kątem ostrym oraz √ -- tg α = 4 3 oblicz wartość wyrażenia √ - --3+sinα 1+cosα .

Zadanie 6

(5 pkt)

Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia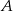
– na każdej kostce wypadła nieparzysta liczba oczek,
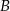– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 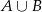A ∪ B .

Zadanie 7

(5 pkt)

W roku 2005 na uroczystości urodzin zapytano jubilata, ile ma lat. Jubilat odpowiedział: „Jeśli swój wiek sprzed 10 lat pomnożę przez swój wiek za 11 lat, to otrzymam rok mojego urodzenia". Ułóż odpowiednie równanie, rozwiąż je i zapisz, w którym roku urodził się ten jubilat.

Zadanie 8

(5 pkt)

Rozwiąż równanie 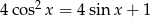2 4co s x = 4 sin x + 1 w przedziale ⟨0,2π ⟩ .

Zadanie 9

(5 pkt)

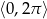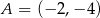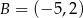Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach A = (− 2,− 4) oraz B = (− 5,2) . Jedno z jego ramion zawiera się w prostej o równaniu 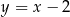y = x − 2 . Oblicz współrzędne trzeciego wierzchołka trójkąta.

Zadanie 10

(5 pkt)

W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.

Zadanie 11

(5 pkt)

W trapezie równoramiennym przekątna ma długość 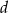i tworzy z dłuższą podstawą kąt o mierze . Oblicz pole tego trapezu.

Rozwiąż on-line Arkusz Wersja PDF