Zestaw użytkownika nr 2233_8331
Zestaw użytkownika
nr 2233_8331
Uzasadnij, że punkty przecięcia dwusiecznych kątów wewnętrznych prostokąta 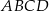 są wierzchołkami kwadratu.
są wierzchołkami kwadratu.

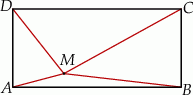
Punkt 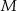 leży wewnątrz prostokąta
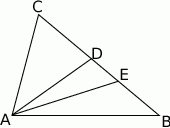
leży wewnątrz prostokąta 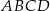 (zob. rysunek). Udowodnij, że
(zob. rysunek). Udowodnij, że 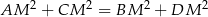 .
.
Dany jest prostokąt 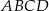 , którego boki mają długości
, którego boki mają długości  i
i 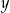 . Punkt
. Punkt 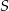 jest punktem przecięcia się przekątnych prostokąta.
jest punktem przecięcia się przekątnych prostokąta.
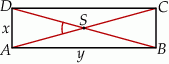
- Wykaż, że pole trójkąta
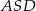 jest cztery razy mniejsze od pola prostokąta
jest cztery razy mniejsze od pola prostokąta 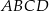 .
. - Wiedząc dodatkowo, że
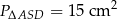 i
i 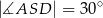 , oblicz pole kwadratu, którego bok ma długość
, oblicz pole kwadratu, którego bok ma długość 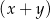 .
.
W prostokącie 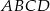 , w którym
, w którym 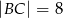 połączono wierzchołek
połączono wierzchołek 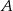 z punktem
z punktem 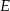 leżącym na boku
leżącym na boku 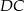 . Odcinek ten przeciął przekątną
. Odcinek ten przeciął przekątną 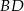 w punkcie
w punkcie 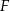 .
.
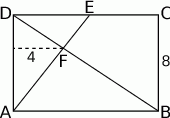
Wiedząc, że odległość punktu 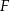 od boku
od boku 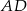 jest równa 4, oraz że
jest równa 4, oraz że 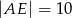 oblicz długość boku
oblicz długość boku 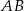 prostokąta.
prostokąta.
W prostokącie, którego krótszy bok ma długość 8 zawarty jest kwadrat o boku równym różnicy
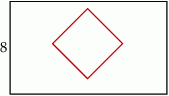
długości boków prostokąta, i którego przekątne są równoległe do boków prostokąta.
- Wyraź pole pozostałe po wycięciu kwadratu z prostokąta jako funkcję dłuższego boku prostokąta. Wyznacz dziedzinę otrzymanej funkcji.
- Wykaż, że różnica pól prostokąta i kwadratu jest zawsze większa od 64.
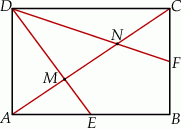
W prostokącie 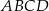 wierzchołek
wierzchołek 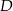 połączono odcinkami ze środkami
połączono odcinkami ze środkami 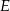 i
i 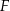 boków
boków 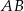 i
i 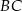 , zaś
, zaś 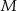 i
i 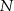 to punkty przecięcia tych odcinków z przekątną
to punkty przecięcia tych odcinków z przekątną 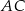 .
.
- Uzasadnij, że odcinki
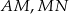 i
i 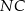 są jednakowej długości.
są jednakowej długości. - Uzasadnij, że trójkąty
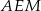 i
i 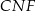 mają równe pola.
mają równe pola.
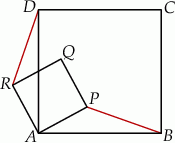
Na bokach 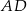 i
i 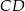 kwadratu
kwadratu 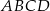 o boku długości 1 wybrano punkty
o boku długości 1 wybrano punkty 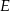 i
i 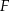 w ten sposób, że
w ten sposób, że 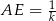 i
i 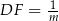 , dla
, dla 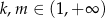 . Niech
. Niech 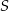 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków 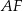 i
i 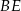
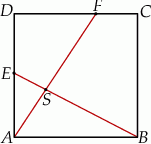
- Wykaż, że jeżeli trójkąt
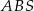 jest prostokątny to
jest prostokątny to 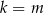 .
. - Oblicz cosinus kąta
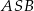 jeżeli
jeżeli 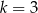 i
i 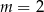 .
.
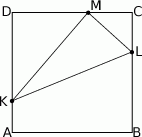
Na bokach 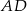 ,
, 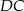 i
i 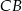 kwadratu
kwadratu 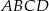 wybrano punkty
wybrano punkty 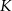 ,
, 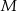 i
i 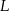 ten sposób, że
ten sposób, że 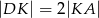 ,
, 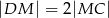 , oraz
, oraz 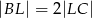 .
.
- Uzasadnij, że trójkąt
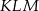 jest prostokątny.
jest prostokątny. - Oblicz tangensy kątów ostrych trójkąta
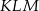 .
.
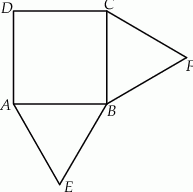
Na zewnątrz kwadratu 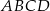 na bokach
na bokach 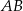 i
i 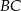 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 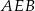 i
i 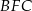 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 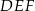 jest równoboczny.
jest równoboczny.
Koło i kwadrat mają równe obwody. Wykaż, że pierwsza z tych figur ma większe pole.
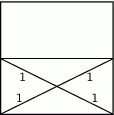
W kwadracie połączono odcinkiem środki przeciwległych boków. Wiedząc, że przekątne tak utworzonych prostokątów dzielą się na odcinki długości 1, oblicz pole wyjściowego kwadratu.
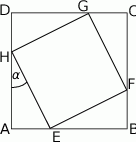
W kwadrat 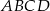 o boku długości 17 wpisano kwadrat
o boku długości 17 wpisano kwadrat 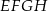 , jak pokazano na rysunku. Wiedząc, że przekątna kwadratu
, jak pokazano na rysunku. Wiedząc, że przekątna kwadratu 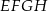 ma długość
ma długość 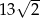 oblicz tangens kąta
oblicz tangens kąta  zaznaczonego na rysunku.
zaznaczonego na rysunku.
Czworokąty  i
i 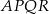 są kwadratami. Udowodnij, że
są kwadratami. Udowodnij, że 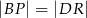 .
.
Na bokach  i
i  równoległoboku
równoległoboku  zbudowano kwadraty
zbudowano kwadraty 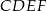 i
i 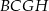 (zobacz rysunek).
(zobacz rysunek).
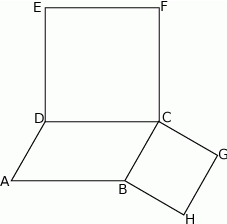
Udowodnij, że 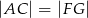 .
.
Prosta przechodząca przez wierzchołek 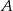 równoległoboku
równoległoboku 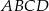 przecina jego przekątną
przecina jego przekątną 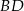 w punkcie
w punkcie 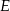 i bok
i bok 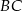 w punkcie
w punkcie 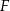 , a prostą
, a prostą 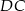 w punkcie
w punkcie 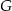 . Udowodnij, że
. Udowodnij, że
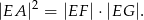
Punkt 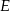 leży na ramieniu
leży na ramieniu 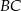 trapezu
trapezu 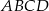 , w którym
, w którym 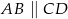 . Udowodnij, że
. Udowodnij, że 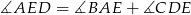 .
.
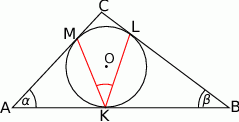
Punkt 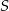 jest środkiem okręgu wpisanego w trapez
jest środkiem okręgu wpisanego w trapez 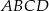 (
(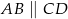 ). Wykaż, że trójkąt
). Wykaż, że trójkąt 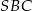 jest prostokątny.
jest prostokątny.
W trapezie 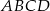 długość podstawy
długość podstawy 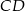 jest równa 18, a długości ramion trapezu
jest równa 18, a długości ramion trapezu 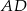 i
i 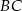 są odpowiednio równe 25 i 15. Kąty
są odpowiednio równe 25 i 15. Kąty 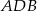 i
i 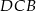 , zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
, zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
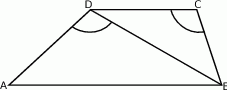
Dany jest trapez 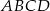 o podstawach
o podstawach 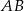 i
i 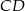 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 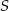 . Wykaż, że
. Wykaż, że 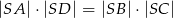 .
.
W trapezie 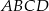 , w którym
, w którym 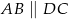 oraz
oraz 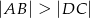 , przekątna
, przekątna 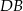 zawiera się w dwusiecznej kąta
zawiera się w dwusiecznej kąta 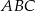 . Wykaż, że
. Wykaż, że 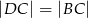 .
.
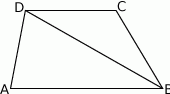
Przekątna trapezu równoramiennego tworzy z dłuższą podstawą kąt 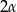 , a z ramieniem kąt
, a z ramieniem kąt  . Wykaż, że stosunek pól trójkątów, na które został podzielony trapez tą przekątną, jest równy
. Wykaż, że stosunek pól trójkątów, na które został podzielony trapez tą przekątną, jest równy 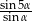 .
.
Dwa przeciwległe boki czworokąta wpisanego w okrąg mają równe długości. Wykaż, że czworokąt ten jest trapezem.
Podstawy trapezu równoramiennego mają długości  i
i 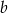 , gdzie
, gdzie 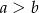 . Z wierzchołka kąta rozwartego trapezu poprowadzono wysokość. Uzasadnij, że wysokość ta dzieli dłuższą podstawę na odcinki o długościach
. Z wierzchołka kąta rozwartego trapezu poprowadzono wysokość. Uzasadnij, że wysokość ta dzieli dłuższą podstawę na odcinki o długościach 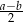 i
i 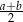 .
.
Wykaż, że istnieją dokładnie dwie liczby naturalne  takie, że trójkąt o bokach
takie, że trójkąt o bokach 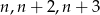 jest rozwartokątny.
jest rozwartokątny.
Udowodnij, że jeżeli w trójkącie dwa kąty nie są równe, to naprzeciw większego z nich leży dłuższy bok.
Wykaż, że pole trójkąta o bokach 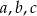 i promieniu
i promieniu 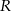 okręgu opisanego na nim jest równe
okręgu opisanego na nim jest równe 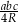 .
.
Odcinki 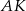 i
i 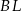 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 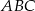 , a punkt
, a punkt 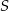 jest punktem ich przecięcia. Uzasadnij, że:
jest punktem ich przecięcia. Uzasadnij, że:
- na czworokącie
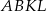 można opisać okrąg;
można opisać okrąg; - okręgi opisane na trójkątach
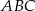 i
i 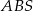 mają promienie równej długości.
mają promienie równej długości.
Wykaż, że jeżeli w trójkącie 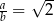 to
to 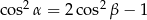 .
.
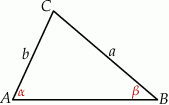
W trójkąt  , w którym
, w którym 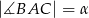 oraz
oraz 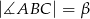 , wpisano okrąg. Punkty
, wpisano okrąg. Punkty 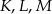 są punktami styczności okręgu odpowiednio z bokami
są punktami styczności okręgu odpowiednio z bokami 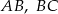 i
i 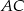 . Wykaż, że
. Wykaż, że 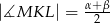 .
.
Dane są dwa trójkąty: 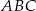 oraz
oraz 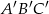 takie, że
takie, że 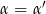 oraz
oraz 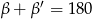 .
.
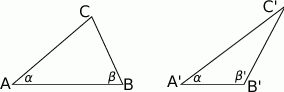
Wykaż, że:
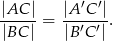
Trójkąty 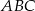 i
i 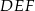 wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
W trójkącie 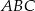 miara kąta
miara kąta 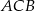 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 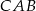 . Dwusieczna kąta
. Dwusieczna kąta 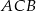 dzieli trójkąt
dzieli trójkąt 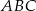 na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta
na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta 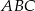 .
.
Uzasadnij wzór na pole trójkąta 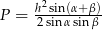 , gdzie
, gdzie  i
i 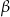 są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość
są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość 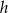 .
.
Punkty 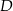 i
i 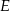 dzielą bok
dzielą bok 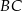 trójkąta
trójkąta 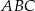 na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta
na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta 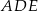 jest trzy razy mniejsze od pola trójkąta
jest trzy razy mniejsze od pola trójkąta 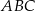 .
.
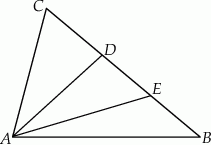
Wykaż, że suma odległości dowolnego punktu wewnętrznego trójkąta od jego wierzchołków jest większa od połowy obwodu trójkąta.
W trójkącie 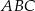 punkt
punkt 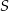 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 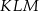 są punktami styczności okręgu wpisanego w trójkąt z bokami
są punktami styczności okręgu wpisanego w trójkąt z bokami 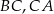 i
i 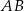 odpowiednio.
odpowiednio.
- Uzasadnij, że na czworokącie
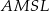 można opisać okrąg.
można opisać okrąg. - Wiedząc, że
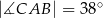 oraz
oraz 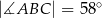 oblicz miary kątów trójkąta
oblicz miary kątów trójkąta 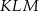 .
.
W trójkącie 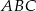 , o bokach długości
, o bokach długości 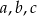 , połączono odcinkiem wierzchołek
, połączono odcinkiem wierzchołek 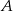 z punktem
z punktem 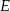 na boku
na boku 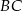 takim, że
takim, że 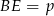 i
i 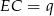 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 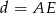 , to
, to 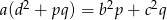 (twierdzenie Stewarta).
(twierdzenie Stewarta).
Wykaż, że jeśli  i
i 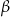 są kątami trójkąta oraz
są kątami trójkąta oraz 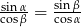 to trójkąt ten jest równoramienny lub prostokątny.
to trójkąt ten jest równoramienny lub prostokątny.
Punkt 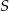 jest punktem przecięcia się wysokości trójkąta ostrokątnego
jest punktem przecięcia się wysokości trójkąta ostrokątnego 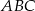 . Wykaż, że jeżeli
. Wykaż, że jeżeli 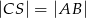 to
to 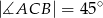 .
.
Na boku 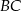 trójkąta
trójkąta 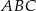 wybrano punkt
wybrano punkt 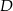 tak, by
tak, by 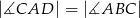 . Odcinek
. Odcinek 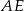 jest dwusieczną kąta
jest dwusieczną kąta 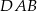 . Udowodnij, że
. Udowodnij, że 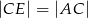 .
.