Zestaw użytkownika nr 2261_6641
WŁASNOŚCI FUNKCJI KLASA I LOPOZIOM ROZSZERZONY
Dana jest funkcja liniowa 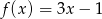 .
.
- Rozwiąż nierówność
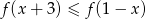 .
. - Podaj maksymalne przedziały monotoniczności funkcji
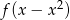 .
.
Liczba  jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 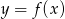 . Wyznacz miejsca zerowe funkcji:
. Wyznacz miejsca zerowe funkcji: 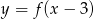 .
.
Wyznacz 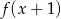 jeżeli
jeżeli 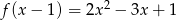 .
.
- Narysuj wykresy funkcji
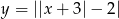 oraz
oraz 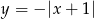 , gdzie
, gdzie 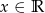 .
. - Wyznacz te wartości parametru
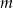 , dla których równanie
, dla których równanie 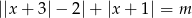 ma dokładnie dwa rozwiązania.
ma dokładnie dwa rozwiązania.
Znajdź wszystkie funkcje liniowe określone na zbiorze 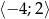 , których zbiorem wartości jest przedział
, których zbiorem wartości jest przedział 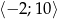 .
.
Zbadaj, na podstawie definicji, monotoniczność funkcji 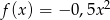 w zbiorze
w zbiorze 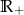 .
.
Wyznacz zbiór wartości funkcji 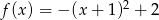 .
.
Funkcja 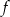 jest określona wzorem
jest określona wzorem
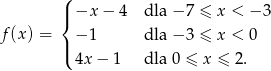
- Podaj dziedzinę funkcji
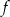 .
. - Podaj jej miejsca zerowe.
- Naszkicuj wykres tej funkcji.
- Podaj zbiór wartości funkcji
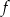 .
.
Wyznacz dziedzinę funkcji  .
.
Wyznacz dziedzinę funkcji określonej wzorem 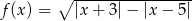 .
.
- Narysuj wykresy funkcji
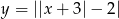 oraz
oraz 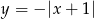 , gdzie
, gdzie 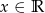 .
. - Wyznacz te wartości parametru
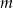 , dla których równanie
, dla których równanie 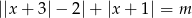 ma dokładnie dwa rozwiązania.
ma dokładnie dwa rozwiązania.
Dana jest funkcja 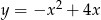 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor
. Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor ![→ u = [− 2,3]](https://img.zadania.info/zad/9470655/HzadT1x.gif) . Narysuj oba wykresy.
. Narysuj oba wykresy.
Naszkicuj wykres funkcji 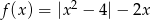 . Określ liczbę rozwiązań równania
. Określ liczbę rozwiązań równania 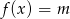 w zależności od wartości parametru
w zależności od wartości parametru 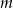 .
.
Funkcja 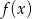 , gdzie
, gdzie 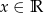 dana jest wzorem
dana jest wzorem
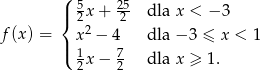
- Narysuj wykres funkcji
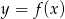 .
. - Odczytaj z wykresu rozwiązanie nierówności
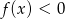 .
.
W prostokątnym układzie współrzędnych narysuj wykres funkcji
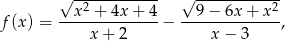
gdzie 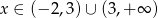 .
.
Dany jest wykres funkcji 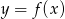 określonej dla
określonej dla 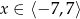 .
.
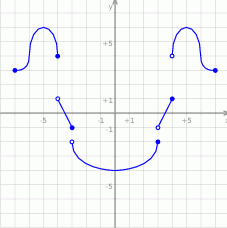
Odczytaj z wykresu:
- rozwiązania równania
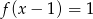 ;
; - miejsca zerowe funkcji
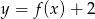 ;
; - maksymalne przedziały monotoniczności funkcji
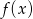 .
.
Naszkicuj wykres funkcji
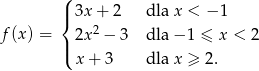
Odczytaj z wykresu maksymalne przedziały monotoniczności funkcji 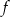 .
.
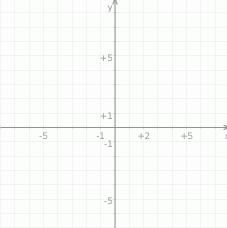
Narysuj wykres funkcji 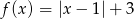 określonej dla
określonej dla 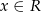 , a następnie na jego podstawie podaj liczbę rozwiązań równania
, a następnie na jego podstawie podaj liczbę rozwiązań równania 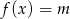 w zależności od parametru
w zależności od parametru 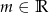 .
.
Naszkicuj wykres funkcji 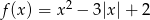 .
.
Funkcja 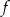 określona jest wzorem
określona jest wzorem 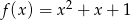 . Znajdź wzór funkcji
. Znajdź wzór funkcji 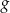 , której wykres otrzymamy:
, której wykres otrzymamy:
- przesuwając wykres funkcji o wektor
![[− 1;− 3]](https://img.zadania.info/zad/2335345/HzadT3x.gif) , a następnie otrzymany wykres przekształcając w symetrii względem osi
, a następnie otrzymany wykres przekształcając w symetrii względem osi 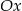 ;
; - dokonując obu przekształceń z poprzedniego punktu, ale w odwrotnej kolejności.
Naszkicuj wykres funkcji: 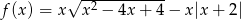 . Wyznacz wartość największą tej funkcji oraz jej maksymalne przedziały monotoniczności.
. Wyznacz wartość największą tej funkcji oraz jej maksymalne przedziały monotoniczności.
Dana jest funkcja 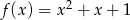 . Napisz wzór funkcji otrzymanej z
. Napisz wzór funkcji otrzymanej z 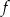 przez
przez
- symetrię względem osi
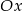 ;
; - symetrię względem osi
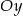 ;
; - symetrię względem punktu
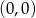 .
.
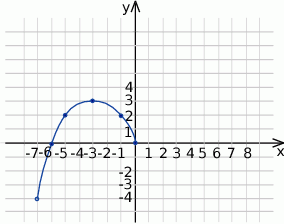
Poniżej znajduje się fragment wykresu funkcji 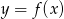 . Wiedząc, że dziedziną tej funkcji jest przedział
. Wiedząc, że dziedziną tej funkcji jest przedział 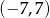 i wykres funkcji jest symetryczny względem punktu
i wykres funkcji jest symetryczny względem punktu 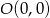 , dorysuj brakującą część wykresu. Następnie na podstawie wykresu funkcji
, dorysuj brakującą część wykresu. Następnie na podstawie wykresu funkcji 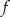 podaj:
podaj:
- zbiór wartości funkcji
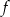
- maksymalne przedziały monotoniczności tej funkcji;
- wszystkie rozwiązania równania
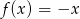 .
.
Naszkicuj wykres funkcji 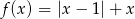 .
.
Narysuj wykres funkcji 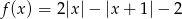 .
.
Naszkicuj wykres funkcji 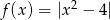 , a następnie określ liczbę rozwiązań równania
, a następnie określ liczbę rozwiązań równania 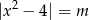 w zależności od wartości parametru
w zależności od wartości parametru 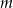 .
.
Dana jest funkcja 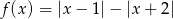 dla
dla 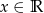 .
.
- Wyznacz zbiór wartości funkcji
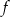 dla
dla 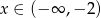 .
. - Naszkicuj wykres tej funkcji.
- Podaj jej miejsca zerowe.
- Wyznacz wszystkie wartości parametru
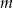 , dla których równanie
, dla których równanie 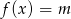 nie ma rozwiązania.
nie ma rozwiązania.
Wyznacz wzór funkcji, której wykres powstaje z wykresu funkcji: 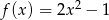 dla
dla 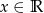 przez przesunięcie o wektor
przez przesunięcie o wektor ![→ u = [−1 ;2]](https://img.zadania.info/zad/7227565/HzadT2x.gif) .
.
Naszkicuj wykres funkcji 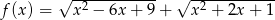 , a następnie korzystając z otrzymanego wykresu ustal liczbę pierwiastków równania
, a następnie korzystając z otrzymanego wykresu ustal liczbę pierwiastków równania 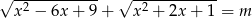 w zależności od parametru
w zależności od parametru 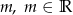 .
.
Narysuj wykres funkcji 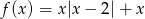 , gdzie
, gdzie 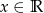 i na jego podstawie odpowiedź na pytania.
i na jego podstawie odpowiedź na pytania.
- Jaki jest zbiór wartości funkcji?
- Dla jakich argumentów wartość funkcji wynosi 2?
- W jakich przedziałach funkcja jest rosnąca?
- Czy funkcja jest parzysta?
Z danego wykresu funkcji 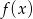 odczytaj
odczytaj
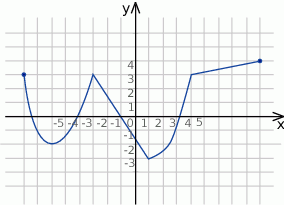
- zbiór wartości funkcji
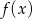 ;
; - rozwiązania równania
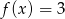 ;
; - maksymalne przedziały monotoniczności funkcji
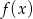 .
.
Narysuj wykres funkcji 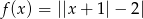 .
.
- Narysuj wykres funkcji
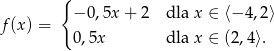
- Na podstawie wykresu funkcji
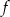 narysuj wykres funkcji
narysuj wykres funkcji 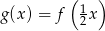 i napisz jej wzór.
i napisz jej wzór. - Na podstawie wykresu funkcji
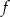 narysuj wykres funkcji
narysuj wykres funkcji 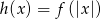 .
.
Narysuj linię o równaniu 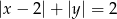 i oblicz jej długość.
i oblicz jej długość.

