Zestaw użytkownika nr 2319_3584
Mała matura 2-II termin3 Listopada 2011Czas pracy: 45 min.Suma punktów: 26
Iloczyn 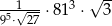 jest równy
jest równy
A) 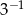 B)
B) 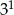 C)
C) 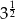 D)
D) 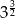
Zbiorem rozwiązań nierówności 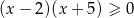 jest
jest
A) 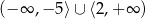
B) 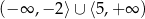
C) 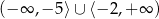
D) 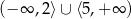
Okrąg o równaniu 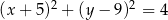 ma środek
ma środek  i promień
i promień  . Wówczas
. Wówczas
A) 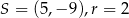 B)
B) 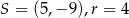 C)
C) 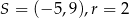 D)
D) 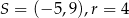
Prosta o równaniu 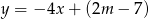 przechodzi przez punkt
przechodzi przez punkt 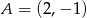 . Wtedy
. Wtedy
A) 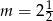 B)
B) 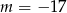 C)
C) 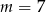 D)
D) 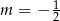
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 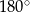 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 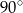 B)
B) 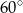 C)
C) 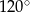 D)
D) 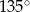
Ciąg arytmetyczny 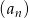 określony jest wzorem
określony jest wzorem 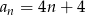 . Zatem suma
. Zatem suma 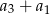 jest równa
jest równa
A) 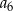 B)
B) 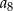 C)
C) 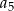 D)
D) 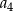
Prosta 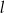 ma równanie
ma równanie 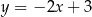 . Równaniem prostej prostopadłej do
. Równaniem prostej prostopadłej do 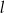 i przechodzącej przez punkt
i przechodzącej przez punkt 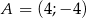 jest:
jest:
A) 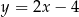 B)
B) 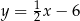 C)
C) 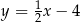 D)
D) 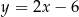
Średnia arytmetyczna danych z tabelki
| Wartość danej | -6 | 6 | -9 | 9 |
| Liczebność danej | 2 | 4 | 1 | 3 |
wynosi
A) 0 B) 3 C) -3 D) 1
Rozwiąż nierówność 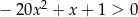 .
.
Kąt  jest ostry
jest ostry 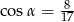 . Oblicz
. Oblicz 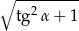 .
.
Dany jest czworokąt 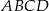 , w którym
, w którym 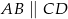 . Na boku
. Na boku 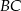 wybrano taki punkt
wybrano taki punkt 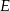 , że
, że 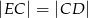 i
i 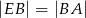 . Wykaż, że kąt
. Wykaż, że kąt 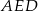 jest prosty.
jest prosty.
Wiadomo, że okrąg jest styczny do prostej o równaniu 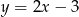 w punkcie
w punkcie 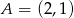 i styczny do prostej o równaniu
i styczny do prostej o równaniu 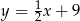 w punkcie
w punkcie 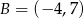 . Oblicz promień tego okręgu.
. Oblicz promień tego okręgu.
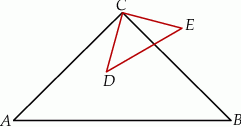
Trójkąty prostokątne równoramienne 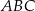 i
i 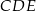 są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku
są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku 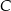 jest prosty). Wykaż, że
jest prosty). Wykaż, że 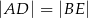 .
.
Grupa rowerzystów jechała ze stałą prędkością do miasta oddalonego o 120 km. Gdyby jechali ze średnią prędkością o 5 km/godz. większą, to przejechaliby tę odległość w czasie o 2 godziny krótszym. Wyznacz średnią prędkość grupy i czas przejazdu.

