Zestaw użytkownika nr 2330_9619
ciągi arytmetyczne i geometryczne poprawaCzas pracy: 45 min.Suma punktów: 30
Między liczby -5 i 49 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
Trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. Ich suma wynosi 18. Jeśli największą z tych liczb zwiększymy o 8, a pozostałych nie zmienimy, to uzyskamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz te liczby.
Pomiędzy liczby 243 i 48 wstaw takie trzy liczby, aby wraz z danymi tworzyły
- ciąg arytmetyczny;
- ciąg geometryczny.
Wykaż, że jeżeli liczby 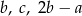 są kolejnymi wyrazami ciągu geometrycznego to liczby
są kolejnymi wyrazami ciągu geometrycznego to liczby 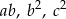 są kolejnymi wyrazami ciągu arytmetycznego.
są kolejnymi wyrazami ciągu arytmetycznego.
Wykaż, że liczby 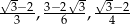 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Liczby 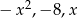 w podanej kolejności tworzą ciąg geometryczny. Oblicz
w podanej kolejności tworzą ciąg geometryczny. Oblicz  .
.
W ciągu geometrycznym 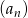 o wyrazach dodatnich spełnione są warunki:
o wyrazach dodatnich spełnione są warunki: 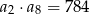 oraz
oraz 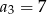 . Iloraz tego ciąg jest równy
. Iloraz tego ciąg jest równy
A) 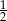 B) 2 C) 4 D)
B) 2 C) 4 D) 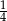
Miary kątów trójkąta tworzą ciąg arytmetyczny o pierwszym wyrazie 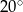 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 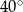 B)
B) 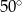 C)
C) 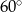 D)
D) 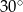
Suma  początkowych wyrazów ciągu arytmetycznego wyraża się wzorem
początkowych wyrazów ciągu arytmetycznego wyraża się wzorem 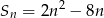 . Wynika stąd, że różnica ciągu jest równa
. Wynika stąd, że różnica ciągu jest równa
A) -8 B) 8 C) 6 D) 4
W ciągu arytmetycznym mamy 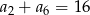 . Oblicz
. Oblicz 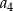 .
.
A) 16 B) 4 C) 8 D) 12
Suma 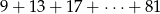 kolejnych wyrazów ciągu arytmetycznego jest równa
kolejnych wyrazów ciągu arytmetycznego jest równa
A) 855 B) 851 C) 1710 D) 859
W ciągu geometrycznym 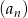 dane są
dane są 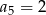 i
i 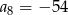 . Wtedy
. Wtedy
A) 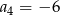 B)
B) 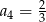 C)
C) 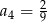 D)
D) 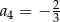
Liczby 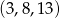 są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
są kolejnymi początkowymi wyrazami ciągu arytmetycznego. Do wyrazów tego ciągu nie należy liczba
A) 103 B) 190 C) 48 D) 168
Ciąg arytmetyczny tworzą liczby
A) 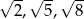 B) -5,-3,-1 C)
B) -5,-3,-1 C) 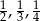 D) 2,4,8
D) 2,4,8
Różnica ciągu arytmetycznego 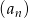 o wyrazie ogólnym
o wyrazie ogólnym 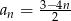 jest równa
jest równa
A) 3 B) -3 C) 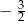 D) -2
D) -2
Pierwszy wyraz ciągu geometrycznego jest równy 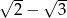 , a drugi wyraz jest równy
, a drugi wyraz jest równy 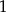 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 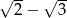 B)
B) 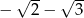 C)
C) 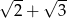 D)
D)