Zestaw użytkownika nr 2381_7700
Trygonometria
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 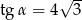 oblicz wartość wyrażenia
oblicz wartość wyrażenia 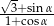 .
.
Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego  jeżeli
jeżeli 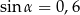 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 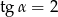 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 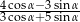 .
.
Uzasadnij, że jeżeli 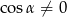 to prawdą jest, że
to prawdą jest, że 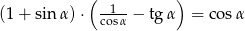 .
.
Wiedząc, że 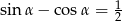 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 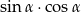 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 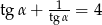 oblicz
oblicz 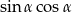 .
.
Porównaj liczby: 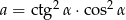 i
i 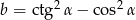 , jeżeli
, jeżeli 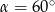 .
.
Posługując się wzorem 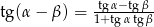 oblicz
oblicz 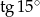 .
.
Sprawdź tożsamość: 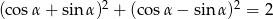 .
.
Kąt  jest kątem ostrym. Wiedząc, że
jest kątem ostrym. Wiedząc, że 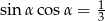 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 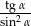 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 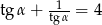 , oblicz
, oblicz 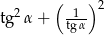 .
.
Wiedząc, że 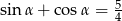 , oblicz
, oblicz 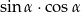 .
.
Kąt  jest ostry
jest ostry 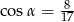 . Oblicz
. Oblicz 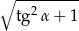 .
.
Kąt  jest ostry oraz
jest ostry oraz 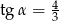 . Oblicz
. Oblicz 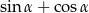 .
.
Wiedząc, że  jest miarą kąta ostrego i
jest miarą kąta ostrego i 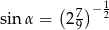 , wyznacz liczbę
, wyznacz liczbę  , dla której
, dla której 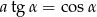 .
.
Kąt  jest ostry i
jest ostry i 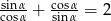 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 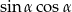 .
.
Oblicz wartość wyrażenia 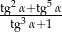 jeżeli
jeżeli 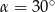 .
.
Kąta  jest ostry oraz
jest ostry oraz 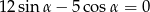 . Oblicz
. Oblicz 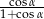 .
.
Kąt  jest ostry i
jest ostry i 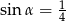 . Oblicz
. Oblicz 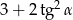 .
.
Oblicz 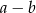 , gdy
, gdy 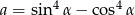 ,
, 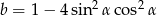 dla
dla 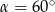 .
.
Wykaż, że 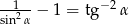 .
.
Kąt  jest kątem ostrym i
jest kątem ostrym i 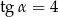 . Wyznacz sinus i cosinus tego kąta.
. Wyznacz sinus i cosinus tego kąta.
Wykaż, że nie istnieje kąt  , taki, że
, taki, że 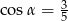 i
i 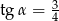 .
.

