Zestaw użytkownika nr 2393_8091
Zestaw użytkownika
nr 2393_8091
Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.
Podaj wzór na wyraz ogólny ciągu 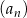 określonego w następujący sposób: ciąg
określonego w następujący sposób: ciąg 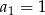 jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
Znajdź  , dla którego liczby
, dla którego liczby 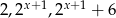 w podanej kolejności tworzą ciąg arytmetyczny.
w podanej kolejności tworzą ciąg arytmetyczny.
Dany jest ciąg 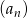 mający tę własność, że dla każdej liczby naturalnej
mający tę własność, że dla każdej liczby naturalnej  suma
suma  początkowych wyrazów tego ciągu jest równa
początkowych wyrazów tego ciągu jest równa 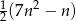 . Oblicz dwudziesty wyraz tego ciągu. Wykaż, że
. Oblicz dwudziesty wyraz tego ciągu. Wykaż, że 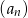 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Dany jest ciąg arytmetyczny 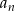 w którym
w którym 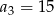 oraz
oraz 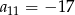 .
.
- Dla jakich
 zachodzi równość
zachodzi równość 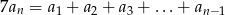 ?
? - Oblicz sumę pięćdziesięciu początkowych, ujemnych wyrazów ciągu
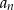 , które są podzielne przez 3.
, które są podzielne przez 3.
Określ wzorem rekurencyjnym ciąg którego pierwszy i drugi wyraz jest równy 3, a każdy następny jest iloczynem dwóch poprzednich.
Rozwiąż układ równań:
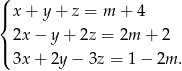
Dla jakich wartości parametru 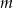 liczby
liczby 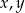 i
i  są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Dany jest ciąg arytmetyczny 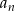 w którym
w którym 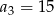 oraz
oraz 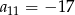 .
.
- Dla jakich
 zachodzi równość
zachodzi równość 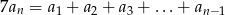 ?
? - Oblicz sumę pięćdziesięciu początkowych, ujemnych wyrazów ciągu
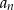 , które są podzielne przez 3.
, które są podzielne przez 3.
Liczby 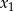 i
i 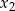 są pierwiastkami równania
są pierwiastkami równania 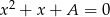 , a liczby
, a liczby 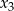 i
i 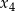 są pierwiastkami równania
są pierwiastkami równania 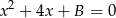 . Wiadomo, że ciąg
. Wiadomo, że ciąg 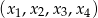 jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz
jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz 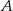 i
i 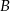 .
.
Długości boków trójkąta tworzą ciąg geometryczny. Jaki warunek spełniać musi iloraz tego ciągu?
Długości boków trójkąta tworzą trzy kolejne wyrazy ciągu arytmetycznego o różnicy 1. Oblicz długości boków tego trójkąta, jeśli jego pole wynosi 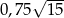 .
.
O ciągu 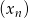 dla
dla 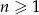 wiadomo, że:
wiadomo, że:
- ciąg
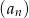 określony wzorem
określony wzorem 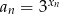 dla
dla 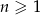 jest geometryczny o ilorazie
jest geometryczny o ilorazie 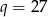 .
. 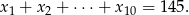
Oblicz 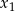 .
.
Długości boków trójkąta są kolejnymi wyrazami rosnącego ciągu geometrycznego o ilorazie 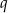 , a cosinus jednego z jego kątów jest równy
, a cosinus jednego z jego kątów jest równy 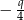 .
.
- Wyznacz
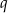 .
. - Wiedząc, że promień okręgu opisanego na tym trójkącie ma długość
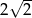 , oblicz pole tego trójkąta.
, oblicz pole tego trójkąta.
Pierwszy, trzeci i jedenasty wyraz ciągu arytmetycznego o różnicy 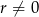 są kolejnymi wyrazami ciągu geometrycznego o ilorazie
są kolejnymi wyrazami ciągu geometrycznego o ilorazie 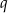 . Dla jakich wartości parametru
. Dla jakich wartości parametru 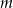 funkcja
funkcja 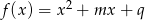 osiąga minimum większe od -196?
osiąga minimum większe od -196?
W trójkąt równoboczny o boku długości  wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.

