Zestaw użytkownika nr 2431_3588
Zestaw użytkownika
nr 2431_3588
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 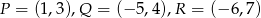 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 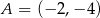 oraz
oraz 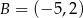 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 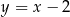 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 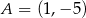 oraz
oraz 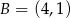 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 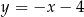 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Dany jest punkt 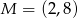 . Wyznacz równanie takiej prostej
. Wyznacz równanie takiej prostej 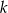 , do której należy punkt
, do której należy punkt 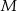 , że na ujemnej półosi
, że na ujemnej półosi 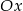 i dodatniej półosi
i dodatniej półosi 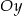 układu
układu 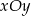 prosta ta wyznacza odcinki
prosta ta wyznacza odcinki 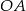 i
i 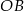 , których suma długości jest równa 6. Oblicz obwód trójkąta
, których suma długości jest równa 6. Oblicz obwód trójkąta 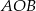 .
.
Wyznacz współrzędne punktu 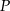 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 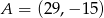 i
i 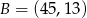 w stosunku
w stosunku 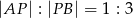 .
.
Punkt 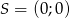 jest środkiem boku
jest środkiem boku 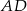 równoległoboku
równoległoboku 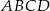 . Wiadomo też, że
. Wiadomo też, że ![−→ AB = [4;3]](https://img.zadania.info/zad/9290117/HzadT3x.gif) oraz
oraz ![−→ BC = [6;2]](https://img.zadania.info/zad/9290117/HzadT4x.gif) . Wyznacz wierzchołki tego równoległoboku.
. Wyznacz wierzchołki tego równoległoboku.
Wykaż, że prosta 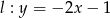 jest styczna do okręgu
jest styczna do okręgu 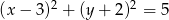 .
.
Dane są punkty 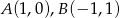 . Punkt
. Punkt 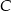 należy do okręgu o równaniu
należy do okręgu o równaniu 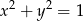 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 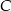 , tak aby pole trójkąta było największe. Oblicz to pole.
, tak aby pole trójkąta było największe. Oblicz to pole.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 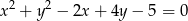 .
.
Ile punktów wspólnych ma prosta 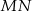 z okręgiem
z okręgiem 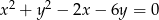 jeśli
jeśli 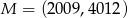 oraz
oraz 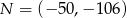 .
.
Punkty 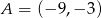 i
i 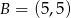 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 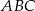 , w którym
, w którym 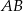 jest przeciwprostokątną. Wyznacz współrzędne wierzchołka
jest przeciwprostokątną. Wyznacz współrzędne wierzchołka 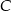 wiedząc, że leży on na osi
wiedząc, że leży on na osi 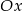 .
.
O ile procent pole koła o promieniu długości 8 jest większe od pola koła wyznaczonego przez okrąg o równaniu 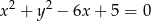 .
.
Wyznacz odległość punktu 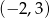 od prostej o równaniu
od prostej o równaniu 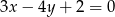 .
.
Napisz równanie okręgu, którego środek należy do osi 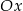 , i który przechodzi przez punkty
, i który przechodzi przez punkty 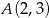 i
i 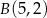 .
.
W układzie współrzędnych dane są dwa punkty: 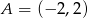 i
i 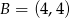 .
.
- Wyznacz równanie symetralnej odcinka
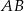 .
. - Prosta
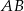 oraz prosta o równaniu
oraz prosta o równaniu 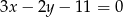 przecinają się w punkcie
przecinają się w punkcie 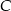 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 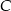 .
.

