Zestaw użytkownika nr 2544_6864
Funkcja kwadratowa
Wyznacz najmniejszą i największą wartość funkcji 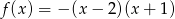 w przedziale
w przedziale 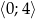 .
.
Wyznacz najmniejszą i największą wartość funkcji 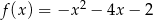 w przedziale
w przedziale 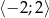 .
.
Określ zbiór wartości funkcji: 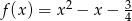 . Dla jakich argumentów funkcja przyjmuje wartości ujemne?
. Dla jakich argumentów funkcja przyjmuje wartości ujemne?
Dana jest funkcja kwadratowa 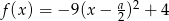
- Dla
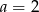 wyznacz postać iloczynową tej funkcji.
wyznacz postać iloczynową tej funkcji. - Dla
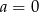 wyznacz te argumenty, dla których funkcja osiąga wartości ujemne.
wyznacz te argumenty, dla których funkcja osiąga wartości ujemne. - Wyznacz
 tak, aby osią symetrii wykresu funkcji była prosta o równaniu
tak, aby osią symetrii wykresu funkcji była prosta o równaniu 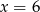 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 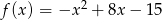 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 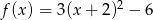 .
.
Zbiorem wartości funkcji kwadratowej 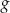 jest przedział
jest przedział 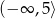 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 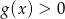 jest przedział
jest przedział 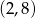 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 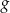 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 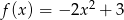 .
.
Zapisz wzór funkcji 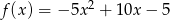 w postaci kanonicznej i iloczynowej.
w postaci kanonicznej i iloczynowej.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 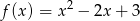 .
.
Wyznacz zbiór wartości funkcji 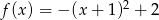 .
.
Miejscami zerowymi funkcji kwadratowej 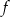 są liczby (-6) oraz 1. Oblicz wartość wyrażenia
są liczby (-6) oraz 1. Oblicz wartość wyrażenia 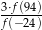 .
.
Rozwiąż równanie 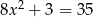 .
.
Rozwiąż równanie: 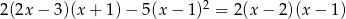 .
.
Rozwiąż nierówność 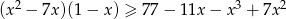 .
.
Rozwiąż nierówność 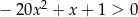 .
.
Dane są funkcje 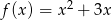 i
i 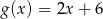 . Rozwiąż nierówność
. Rozwiąż nierówność 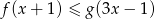 .
.
Rozwiąż nierówność: 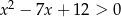 .
.
Funkcje 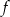 i
i 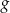 dane są wzorami
dane są wzorami 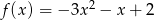 ,
, 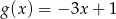 . Wyznacz zbiór argumentów
. Wyznacz zbiór argumentów  , dla których funkcja
, dla których funkcja 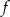 przyjmuje wartości większe od funkcji
przyjmuje wartości większe od funkcji 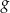 .
.
Rozwiąż nierówność 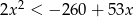 . Podaj wszystkie liczby całkowite, które spełniają tę nierówność.
. Podaj wszystkie liczby całkowite, które spełniają tę nierówność.
Rozwiąż nierówność: 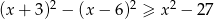 .
.

