Zestaw użytkownika nr 2668_3062
Zestaw użytkownika
nr 2668_3062
W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm. Oblicz pole tego trójkąta.
Boki trójkąta mają długości 4, 8 i 10.
- Oblicz cosinus i tangens kąta leżącego naprzeciwko najkrótszego boku.
- Oblicz długość środkowej poprowadzonej do najdłuższego boku.
Suma długości dwóch boków trójkąta wynosi 6 cm, a miara kąta pomiędzy tymi bokami wynosi 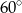 . Jaką najmniejszą wartość ma obwód tego trójkąta.
. Jaką najmniejszą wartość ma obwód tego trójkąta.
Długości dwóch boków trójkąta są równe 1 i 4, a miara kąta zawartego między nimi wynosi 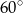 .
.
- Oblicz pole tego trójkąta.
- Oblicz promień okręgu opisanego na tym trójkącie.
- Oblicz promień okręgu wpisanego w ten trójkąt.
Na boku 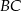 trójkąta równobocznego
trójkąta równobocznego 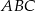 obrano taki punkt
obrano taki punkt 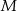 , że pole trójkąta
, że pole trójkąta 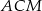 jest cztery razy mniejsze od pola trójkąta
jest cztery razy mniejsze od pola trójkąta 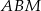 . Oblicz sinusy kątów
. Oblicz sinusy kątów 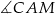 i
i 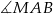 .
.
Wykaż, że jeżeli  i
i 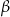 są kątami trójkąta oraz
są kątami trójkąta oraz 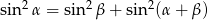 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny.
Wykaż, że istnieją dokładnie dwie liczby naturalne  takie, że trójkąt o bokach
takie, że trójkąt o bokach 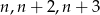 jest rozwartokątny.
jest rozwartokątny.
W trójkącie 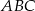 dane są długości boków:
dane są długości boków: 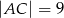 ,
, 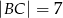 . Wiadomo też, że miara kąta
. Wiadomo też, że miara kąta 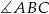 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 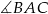 . Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.
. Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.
Dany jest trójkąt o bokach długości 7,8,9.
- Oblicz promień okręgu wpisanego w ten trójkąt.
- Oblicz sumę sinusów kątów tego trójkąta.
Dany jest trójkąt o bokach długości 4 (podstawa trójkąta), 5 i 6 – boki trójkąta. Przez punkt przecięcia się środkowych trójkąta prowadzimy prostą równoległą do podstawy. Oblicz obwód trójkąta którego podstawą jest ta prosta.
W trójkącie 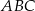 dane są długości boków:
dane są długości boków: 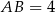 ,
, 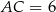 ,
, 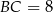 . Oblicz długości odcinków, na jakie dzieli bok
. Oblicz długości odcinków, na jakie dzieli bok 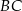 wysokość opuszczona z wierzchołka
wysokość opuszczona z wierzchołka 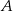 .
.
W trójkącie 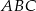 poprowadzono wysokości
poprowadzono wysokości 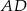 i
i 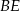 oraz dwusieczną
oraz dwusieczną 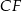 . Wiedząc, że
. Wiedząc, że 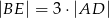 oblicz stosunek pól trójkątów
oblicz stosunek pól trójkątów 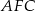 i
i 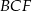 .
.

